REGRESIÓN             

INTRODUCCIÓN
REGRESIÓN DE LA MEDIA
REGRESIÓN MÍNIMO-CUADRÁTICA
REGRESIÓN LINEAL 
        RECTA DE REGRESIÓN Y/X
        RECTA DE REGRESIÓN X/Y
        COEFICIENTES DE REGRESIÓN
        RESIDUOS
BONDAD DEL AJUSTE
        VARIANZA RESIDUAL
        VARIANZA DE LA REGRESIÓN
        COEFICIENTE DE DETERMINACIÓN
REGRESIÓN MÍNIMO CUADRÁTICA NO-LINEAL
        REGRESIÓN PARABÓLICA
        REGRESIÓN POTENCIAL
      REGRESIÓN EXPONENCIAL

PROGRAMAS

INTRODUCCIÓN

En el marco del análisis estadístico multidimensional interesa, en gran medida, descubrir la interdependencia o la relación existente entre dos o más de las características analizadas.

La dependencia entre dos ( o más ) variables puede ser tal que se base en una relación funcional (matemática ) exacta, como la existente entre la velocidad y la distancia recorrida por un móvil; o puede ser estadística. La dependencia estadística es un tipo de relación entre variables tal que conocidos los valores de la ( las) variable (variables ) independiente(s) no puede determinarse con exactitud el valor de la variable dependiente, aunque si se puede llegar a determinar un cierto comportamiento (global) de la misma. (Ej . : la relación existente entre el peso y la estatura de los individuos de una población es una relación estadística) .

Pues bien, el análisis de la dependencia estadística admite dos planteamientos ( aunque íntimamente relacionados) :

El estudio del grado de dependencia existente entre las variables que queda recogido en la teoría de la correlación.

La determinación de la estructura de dependencia que mejor exprese la relación, lo que es analizado a través de la regresión .

Una vez determinada la estructura de esta dependencia la finalidad última de la regresión es llegar a poder asignar el valor que toma la variable Y en un individuo del que conocemos que toma un determinado valor para la variable X (para las variablesX1,X2,..., Xn ).

En el caso bidimensional, dadas dos variables X e Y con una distribución conjunta de frecuencias ( xi, yj ,nij ), llamaremos regresión de Y sobre X ( Y/X) a una función que explique la variable Y para cada valor de X, y llamaremos regresión de X sobre Y (X/Y) a una función que nos explique la variable X para cada valor de Y.(Hay que llamar la atención, como se verá más adelante, que estas dos funciones, en general, no tienen por qué coincidir).

REGRESIÓN DE LA MEDIA.

La primera aproximación a la determinación de la estructura de dependencia entre una variable Y y otra u otras variables X (X1,X2,..., Xn) es la llamada regresión de la media (regresión I) (regresión en sentido estricto).

Consideremos el caso bidimensional:

Regresión Y/X (en sentido estricto) (de la media).

Consistirá en tomar como función que explica la variable Y a partir de la X a una función que para cada valor de X , xi, le haga corresponder (como valor de Y ) el valor de la media de la distribución de Y condicionada a xi .La función de regresión quedaría explicitada por el conjunto de puntos: ( x_i ,y/x_i ).

Regresión X/Y (en sentido estricto) (de la media).

Consistirá en tomar como función que explica la variable X a partir de la Y a una función que para cada valor de Y , y_j, le haga corresponder (como valor de X ) el valor de la media de la distribución de X condicionada a Yj .La función de regresión quedaría explicitada por el conjunto de puntos: ( x/y_j ,y_j ).

REGRESIÓN MÍNIMO-CUADRÁTICA

Consiste en explicar una de las variables en función de la otra a través de un determinado tipo de función (lineal, parabólica, exponencial, etc.), de forma que la función de regresión se obtiene ajustando las observaciones a la función elegida, mediante el método de Mínimos-Cuadrados (M.C.O.).

Elegido el tipo de función ¦ ( ) la función de regresión concreta se obtendrá

minimizando la expresión:

                        (y_j - ¦ (x_i ) ) ². n_ij en el caso de la regresión de Y/X

            (x_i - ¦ (y_j ) ) ². n_ij en el caso de la regresión de X/Y

Puede probarse que es equivalente ajustar por mínimos cuadrados la totalidad de las observaciones (toda la nube de puntos) que realizar el ajuste de los puntos obtenidos por la regresión de la media; de forma que la regresión mínimo-cuadrática viene ser, en cierto modo, la consecución de una expresión analítica operativa para la regresión en sentido estricto.

REGRESIÓN LINEAL (ir a script de regresión)

A pesar de la sencillez de las funciones lineales tiene una importancia fundamental. La regresión será lineal cuando la función de ajuste seleccionada sea una función lineal, una recta, se habla también de recta de regresión.

Recta de regresión de Y/X (M.C.O)

Pretendemos obtener como función de regresión que nos explique la variable Y en función de los valores de X una función lineal, con el criterio de que minimice los cuadrados de las diferencias entre los valores reales y los teóricos (según la regresión).

La función de regresión a obtener es y* = a + b X con la pretensión de que
                         (y_j - (a+b x_i) ) ².n_ij sea mínima .

Habrá que encontrar los valores de los parámetros a y b que minimizan esa expresión. Es decir que anulan simultáneamente las derivadas parciales de la función:

y (a,b)= (y_j - (a+b x_i) ) ².n_ij: (Sistema de ecuaciones normales)

= 0	2 (yj -a-b xi ) . nij (-1)= 0
= 0	2[ yj -a-b xi ) . nij ].[- xi nij ] = 0

yj nij =anij +b xi nij
yj xi nij = a xi nij +b xi2 nij

(*1)

                                restando la segunda ecuación por la primera multiplicada por -x, quedará:

Sxy=b S2x (*2)

de forma que de (*1) y de (*2) se concluye que los valores de a y b que minimizan los cuadrados de los residuos y que, por tanto son los parámetros del ajuste mínimo-cuadrático serán:

                    La ecuación de la recta de regresión Y/X quedará, por lo tanto como:

    De (*1) , o de la propia ecuación de la recta se deduce que la recta de regresión de Y/X pasa por el centro de gravedad de la distribución .

Otra expresión alternativa de la recta de regresión de regresión Y/X es:

Recta de regresión de X /Y (M.C.O)

Pretendemos obtener, ahora la regresión lineal que nos explique la variable X en función de los valores de Y.El procedimiento de obtención será, en todo análogo, al anterior, pero ahora la función de regresión a obtener será:

                                         x* = a' + b' Y con la pretensión de que:

             (x_i - (a'+b' y_j) ) ².n_ij sea mínima .

Habrá que encontrar los valores de los parámetros a' y b' que minimizan esa expresión.Es decir que anulan simultaneamente las derivadas parciales de la función:
y (a' , b' )= (x_i - (a'+b' y_j) ) ².n_ij : (Sistema de ecuaciones normales)

= 0	2 (xi -a'-b' yj ) . nij (-1)= 0
= 0	2 [ xi -a'-b' yj ) . nij ].[- yj nij ] = 0

xi nij =a' nij +b' yj nij
yj xi nij = a xi nij +b xi2 nij

(*1')

                                    restando la segunda ecuación por la primera multiplicada por -y, quedará:

Sxy=b' S2y (*2')

de forma que de (*1') y de (*2') se concluye que los valores de a' y b'que minimizan los cuadrados de los residuos y que, por tanto son los parámetros del ajuste mínimo-cuadrático serán:

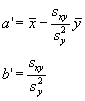
                                La ecuación de la recta de regresión Y/X quedará, por lo tanto como:

De (*1) , o de la propia ecuación de la recta se deduce que la recta de regresión de Y/X pasa por el centro de gravedad de la distribución .

Otra expresión alternativa de la recta de regresión de regresión Y/X es:

  Coeficientes de regresión

Se llama coeficiente de regresión a la pendiente de la recta de regresión:

                                            en la regresión Y/X : b = S_xy / S_x² 

                                            en la regresión X/Y b' = S_xy / S_y²  

El signo de ambos coincidirá con el de la covarianza, indicándonos la tendencia (directa o inversa a la covariación).Es interesante hacer notar que b.b'= r²

Nota.

Realizada la regresión (por ejemplo la Y/X, aunque ocurre igual con la X/Y),

podemos considerar el resultado obtenido Y* como una variable (que se obtiene en función de los valores de X) (variable regresión) de manera que:

                                     Y* es tal que y*_i = a + b x_i

Puede igualmente considerarse otra variable e (llamada residuo) que resulta ser, precisamente la diferencia entre el valor real de la variable regresando (Y) y el valor teórico de la regresión (Y*):

                                                                    e_i=y_i-y*_i

De el resultado de la recta de regresión es obvio que la media de la variable regresión coincide con la media de la variable regresando: .

Y de este resultado se deduce que la media de los residuos o errores es cero:

Además es sencillo probar que las variables regresión y residuo están incorrelacionadas y por tanto:

BONDAD DEL AJUSTE (Varianza residual, varianza de la regresión y coeficiente de determinación)

Por bondad del ajuste hay que entender el grado de acoplamiento que existe entre los datos originales y los valores teóricos que se obtienen de la regresión. Obviamente cuanto mejor sea el ajuste, más útil será la regresión a la pretensión de obtener los valores de la variable regresando a partir de la información sobre la variable regresora .

Obtener indicadores de esta bondad de ajuste es fundamental a la hora de optar por una regresión de un determinado tipo u otro.

Puesto que la media de los residuos se anula, el primer indicador de la bondad del ajuste (no puede ser el error medio) será el error cuadrático medio, o varianza del residuo, o varianza residual :

Considerando la regresión Y/X:

Que será una cantidad mayor o igual que cero.De forma que cuanto más baja sea mejor será el grado de ajuste.Si la varianza residual vale cero el ajuste será perfecto (ya que no existirá ningún error ).

                        Del hecho de que y_i=y*_i+e_i ,y de que las variables y* ý e están incorrelacionadas se tiene que:

                    Donde S²_y* es la llamada varianza de la regresión y supone la varianza de la variable regresión:

Igualdad fundamental anterior de la que se deduce que la varianza total de la variable y puede descomponerse en dos partes una parte explicada por la regresión( la varianza de la regresión) y otra parte no explicada (la varianza residual).

Considerando que la varianza nos mide la dispersión de los datos este hecho hay que entenderlo como que la dispersión total inicial queda, en parte explicada por la regresión y en parte no.Cuanto mayor sea la proporción de varianza explicada (y menor la no explicada) tanto mejor será el ajuste y tanto más útil la regresión.

A la proporción de varianza explicada por la regresión se le llama coeficiente de determinación ( en nuestro caso lineal):                

que evidentemente estará siempre comprendido entre 0 y 1 y, en consecuencia, da cuenta del tanto por uno explicado por la regresión.

Una consecuencia importante en la práctica es que la varianza residual será obviamente:

Es sencillo probar que en el caso lineal que nos ocupa el coeficiente de determinación coincide con el cuadrado del coeficiente de correlación: R² = r²

Con lo cual la varianza residual y la varianza debida a la regresión pueden calcularse a partir del coeficiente de correlación:

REGRESIÓN MÍNIMO CUADRÁTICA NO-LINEAL

La regresión mínimo-cuadrática puede plantearse de forma que la función de ajuste se busca no sea una función lineal. El planteamiento general sería similar, aunque obviamente habría que minimizar el cuadrado de los residuos entre los datos originales y los valor teóricos obtenibles a través de la función no-lineal considerada.

Regresión parabólica .Desarrollaremos someramente la regresión Y/X y debe quedar claro que la regresión X/Y resultaría análoga.

Supongamos para simplificar que los datos no están agrupados por frecuencias.

En tal caso, obtener la función parabólica y* = a₀+a₁x+a₂ x² se llevará a cabo determinado los valores de los tres parámetros a₀,a₁,a₂ que minimicen :

                            y (a₀,a₁,a₂)=S (yi- (a₀+a₁x+a₂ x²)) ²

Igualando a cero las tres derivadas parciales se obtendrá las ecuaciones normales, que convenientemente manipuladas acaban siendo:

yj =N a0 + a1 xi + a2xi2

yjxi = a0 xi + a1 xi2 + a2 xi3

yjxi2 = a0 xi2 + a1 xi3 + a2 xi4

Sistema de ecuaciones del que se pueden despejar los valores de los coeficientes de regresión.

Regresión exponencial

Será aquella en la que la función de ajuste será una función exponencial del tipo

                                y = a.b^x

La regresión exponencial aunque no es lineal es linealizable tomando logaritmos ya que haciendo el cambio de variable
v = log y tendremos que la función anterior nos generaría:

                                    v = log y = log( a.bx) = log a + x log b

la solución de nuestro problema vendría de resolver la regresión lineal entre v ý x, y una vez obtenida supuesta ésta:
v* = A + B x ; obviamente la solución final será:

a = antilog A y b = antilog B.

Regresión potencial.

Será aquella en la que la función de ajuste sea una función potencial del tipo:

                                                                y = a. x^b

también en este caso se resuelve linealizando la función tomando logaritmos ya que:

                                                log y = log a + b log x

Considerando las nuevas variables v = log y u= log x resolveríamos la regresión lineal entre ellas de forma que si el resultado fuera: v*= A +B u

La solución final quedaría como a= antilog A y b= B