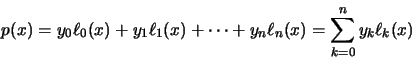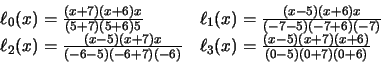

Next: 7.2 Interpolación de splines
Up: 7. Interpolación
Previous: 7. Interpolación
7.1 Polinomios de interpolación de Lagrange
Un polinomio de interpolación de Lagrange, p, se define en la forma:
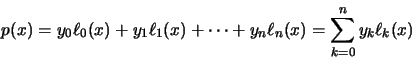 |
(68) |
en donde
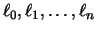 son polinomios que
dependen sólo de los nodos tabulados
son polinomios que
dependen sólo de los nodos tabulados
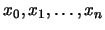 ,
pero
no de las ordenadas
,
pero
no de las ordenadas
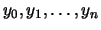 .
La fórmula general del
polinomio
.
La fórmula general del
polinomio 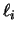 es:
es:
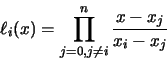 |
(69) |
Para el conjunto de nodos
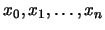 ,
estos polinomios
son conocidos como funciones cardinales. Utilizando estos
polinomios en la ecuación (68) obtenemos la forma
exacta del polinomio de interpolación de Lagrange.
,
estos polinomios
son conocidos como funciones cardinales. Utilizando estos
polinomios en la ecuación (68) obtenemos la forma
exacta del polinomio de interpolación de Lagrange.
Ejemplo: Suponga la siguiente tabla de datos:
|
x |
5 |
-7 |
-6 |
0 |
|
y |
1 |
-23 |
-54 |
-954 |
Construya las funciones cardinales para el conjunto de nodos dado y
el polinomio de interpolación de Lagrange correspondiente.
Las funciones cardinales, empleando la expresión (69),
resultan ser:
El polinomio de interpolación de Lagrange es:


Next: 7.2 Interpolación de splines
Up: 7. Interpolación
Previous: 7. Interpolación
Wladimiro Diaz Villanueva
1998-05-11