2.3 Propagación de errores

Cuando se resuelve un problema matemático por métodos numéricos y aunque las operaciones se lleven a cabo exactamente, obtenemos una aproximación numérica del resultado exacto. Es importante tratar de conocer el efecto que sobre el resultado final del problema tiene cada una de las operaciones realizadas.

Para estudiar como se propaga en error, veamos cual es el efecto que cada una de las operaciones básicas tiene sobre el error final cuando se aplican sobre dos números $x_{1} \pm \varepsilon_{a}(x_{1})$ y $x_{2} \pm \varepsilon_{a}(x_{2})$ :

$$\varepsilon_{a}(x_{1} + x_{2}) \varepsilon_{a}(x_{1}) + \varepsilon_{a}(x_{2})$$ = (10)

$$\varepsilon_{a}(x_{1} - x_{2}) \varepsilon_{a}(x_{1}) + \varepsilon_{a}(x_{2})$$ = (11)

$$\varepsilon_{r}(x_{1} x_{2}) \varepsilon_{r}(x_{1}) + \varepsilon_{r}(x_{2})$$ = (12)

$$\varepsilon_{r}(\frac{x_{1}}{x_{2}}) \varepsilon_{r}(x_{1}) + \varepsilon_{r}(x_{2})$$ = (13)

Cuando el problema consiste en calcular el resultado y = f(x)tenemos la siguiente fórmula aproximada de propagación del error:

$$\varepsilon_{a}(y) = \vert f'(x)\vert\varepsilon_{a}(x)$$ (14)

En el caso más general, en que una función depende de más de una variable ( $y = f(x_{1},x_{2},\dots,x_{n})$), la fórmula aproximada de propagación del error maximal es:

$$\varepsilon_{a}(y) = \sum_{i = 1}^{n}\vert\frac{\partial}{\... ... x_{i}} f(x_{1},x_{2},\dots,x_{n})\vert\varepsilon_{a}(x_{i})$$ (15)

Ejemplo 3: Determinar el error máximo cometido en el cálculo y = x₁ x₂² para $x_{1} = 2.0 \pm 0.1$ y $x_{2} = 3.0 \pm 0.2$.

Solución: El error cometido, de acuerdo con la ecuación (15), se puede calcular mediante:

$$\begin{eqnarray*}\varepsilon_{a}(y) & = & \vert\frac{\partial}{\partial x_{1}} (... ...on_{a}(x_{1}) + \vert 2 x_{1} x_{2}\vert \varepsilon_{a}(x_{2}) \end{eqnarray*}$$

Sustituyendo valores, obtenemos:

$$\begin{eqnarray*}y & = & 2.0 \cdot (3.0)^{2} = 18.00 \\ \varepsilon_{a}(y) & = & (3.0)^{2} \cdot 0.1 + 2 \cdot 2.0 \cdot 3.0 \cdot 0.2 = 3.3 \end{eqnarray*}$$

Por lo que el resultado final se debe expresar como:

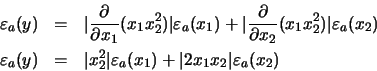
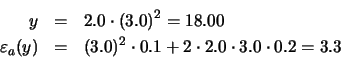
Ejemplo 4: Sea el siguiente sistema de ecuaciones lineales:

$$\left. \begin{array}{rrr} x + ay & = & 5 \\ bx + 2y & = & d \end{array} \right\} \nonumber$$

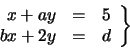
en donde $a = 1.000 \pm 0.002$; b = 1 / a y d = b - a¿Con qué exactitud podemos determinar el producto xy?

Solución: Primero resolveremos el sistema de ecuaciones por reducción:

$$\begin{eqnarray*}x & = & \frac{(10 - ad)}{(2 - ab)} \\ y & = & \frac{(d - 5b)}{(2 - ab)} \end{eqnarray*}$$

Ecuaciones que conducen a la siguiente expresión para el producto:

$$xy = \frac{\overbrace{(10 - ad)}^{A} \overbrace{(d - 5b)}^{B}}{\underbrace{(2 - ab)^2}_{C}}$$ (16)

Resolveremos ahora el problema por dos métodos. Primero, calcularemos el error asociado a cada una de las variables y los términos de la expresión anterior:

$$\begin{array}{ll} a = 1.000; & \varepsilon_{a}(a) = 0.002 \\... ...varepsilon_{a}(C)}{C^{2}} = 680\varepsilon_{a}(a) \end{array}$$

Sustituyendo valores, obtenemos el siguiente resultado:

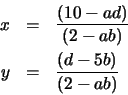
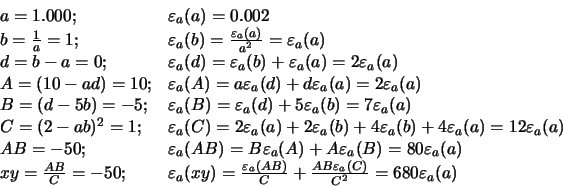
Una forma mucho más adecuada de resolver este problema consiste en sustituir en la expresión (16) los valores de b y d por sus correspondientes expresiones en función de a. Sustituyendo y operando, obtenemos que el producto y el error asociado vienen dados por:

$$\begin{eqnarray*}xy & = & -(a^{2} + 13a + \frac{36}{a}) \\ \varepsilon_{a}(xy)... ...rt 2a\vert + 13 + \vert\frac{36}{a^{2}}\vert)\varepsilon_{a}(a) \end{eqnarray*}$$

que, sustituyendo valores, conduce al resultado:

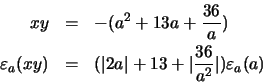
Si ambos resultados son correctos ¿Por qué el error es mucho menor en el segundo caso que en el primero? La respuesta es simple: en el segundo caso hemos eliminado operaciones intermedias, permitiendo que algunos errores se cancelen mutuamente. En general, cuanto menor sea el número de pasos intermedios que efectuemos para alcanzar la solución, menor será el error cometido.