ANTERIOR	EL ESPACIO Y EL TIEMPO	SIGUIENTE

En la página anterior hemos concluido que la relación entre mis sensaciones y mis experiencias consiste en que éstas son una interpretación de aquéllas, y que en esta interpretación podemos aislar una primera fase en la que las sensaciones son interpretadas en términos de la geometría tridimensional euclídea, lo cual da lugar a lo que hemos llamado intuiciones. Sin embargo, en nuestra primera aproximación al concepto de intuición hemos pasado por alto que mi entendimiento no sólo interpreta mis sensaciones en términos espaciales, sino también temporales. Del mismo modo que mi entendimiento me dice que aquella luz roja que percibo proviene de un objeto situado a unos metros delante de mí, mientras que aquella otra luz roja corresponde a otro objeto similar pero más alejado, también me dice que el objeto cercano ha cambiado su luz roja por otra verde un poco antes de que lo hiciera el más alejado, así como que, apenas el más cercano ha pasado de rojo a verde, varios objetos que estaban parados han empezado a moverse. Si veo un objeto en movimiento, estoy teniendo una única intuición que puedo describir en términos de la geometría del espacio y del tiempo. El tiempo tiene su propia geometría, que es mucho más simple que la del espacio, ya que tiene una única dimensión. Un objeto puede moverse en muchas direcciones espaciales, pero en el tiempo sólo puedo moverme hacia adelante o hacia atrás. (No estamos afirmando que podamos viajar al pasado, sino únicamente que podemos preguntarnos, por ejemplo, dónde estaba un objeto antes o después de pasar por un cierto lugar, y no hay más opciones.)

Una afirmación que puedo asegurar sin lugar a dudas por su carácter trascendental, al igual que sucede con "yo pienso", "yo percibo", "yo intuyo", etc. es que todas mis intuiciones han de ocupar necesariamente un lugar en el tiempo. Dicho de otro modo: mi entendimiento no puede proporcionarle una intuición a mi conciencia sin situarla en el tiempo. Como siempre, esto es así porque no puedo concebir otra posibilidad. Es algo que puedo afirmar sin que medie razonamiento alguno porque la posibilidad de que sea falso es absolutamente inconcebible.

En cambio, no todas las intuiciones tienen por qué estar situadas en el espacio. Ello nos lleva a distinguir entre intuiciones externas, que son las que se sitúan en el espacio y en el tiempo, e intuiciones internas, que son las que se sitúan sólo en el tiempo. Entre las intuiciones internas podemos contar mi "voz interior", esto es, la voz con la que me hablo cuando hago lo mismo que si fuera a hablar pero no pronuncio palabra alguna. Si, por ejemplo, recito mentalmente un poema, puedo decir que en un momento dado he "dicho" Nadie puede ser dichoso, que a continuación he "dicho" señora, ni desdichado y que después he "dicho" sino que os haya mirado. Cada palabra que he "dicho" ocupa un lugar en el tiempo, pero no en el espacio. En cambio, cuando oigo hablar a otra persona, o incluso si hablo yo mismo realmente, al sonido que percibo le puedo asignar un punto de procedencia en el espacio. (Otra cosa es que atine al identificarlo o no.)

Más en general, son intuiciones internas todos mis pensamientos, incluso si no están articulados en palabras. Si a las cinco en punto he decidido coger un libro, aunque nunca haya pronunciado, ni siquiera mentalmente, las palabras "voy a coger ese libro", no por ello deja de ser cierto que a las cinco en punto mi conciencia "se ha llenado" con una intuición, a saber, con una volición que me ha determinado a coger un libro y ponerme a leer. Si en un momento veo algo que causa en mí el efecto de sentirme feliz, y esa felicidad me dura dos horas, puedo decir que esa sensación de felicidad era una intuición interna, debidamente ubicada en el tiempo, aunque no en el espacio. (Estaría fuera de lugar que alguien afirmara que mi felicidad ocupa la porción de espacio ocupada por mi cerebro, ya que no hay nada en mi conciencia que vincule mi sensación de felicidad con mi cerebro.)

Acabamos de decir que los pensamientos son intuiciones, pero esto no debe inducirnos a confundir cosas muy distintas. Por ejemplo, si me preguntan cuántas sillas hay en el salón de mi casa y yo, que acabo de comprarlas, respondo que "ocho" porque recuerdo que he comprado ocho sillas, entonces puedo decir que he tenido la intuición de pensar "en mi salón hay ocho sillas", pero no he tenido intuición alguna de mi salón. Sin embargo, también podría haber respondido a la pregunta recordando cómo es mi salón y contando las sillas: "Hay cuatro alrededor de la mesa, dos contra una pared lateral y otras dos contra la pared del fondo." En tal caso, en mi conciencia ha aparecido una intuición (externa) de mi salón, que a su vez ha sido usada por mi entendimiento para generar el pensamiento (la intuición interna) "en mi salón hay ocho sillas". En resumen: los pensamientos son intuiciones (internas), pero no todas las intuiciones son pensamientos. Formarse una imagen de algo es algo muy diferente a pensar en ello.

En el ejemplo precedente hemos mencionado la capacidad que tengo de formarme una imagen intuitiva de algo (como mi salón) aunque no esté presente ante mí, es decir, de algo que mi entendimiento, en su interpretación ulterior más allá de la mera intuición, calificará de irreal. En general, llamaremos intuiciones formales a aquellas intuiciones que carecen de un contenido sensitivo. Cuando pienso en el salón de mi casa (sin verlo, pero formándome una imagen intuitiva) o, por poner un ejemplo más simple, cuando me imagino un cubo para contar sus vértices y concluir que tiene ocho, estoy teniendo intuiciones sin tener sensación alguna. No obstante, no todas las intuiciones internas son formales. Por ejemplo, el miedo, la alegría, etc., son sensaciones que puedo situar en el tiempo, pero no en el espacio. A este respecto conviene hacer una precisión: Intuir es intuir objetos (esto lo analizaremos con más detenimiento en páginas posteriores), de modo que si, por ejemplo, oigo sonar el teléfono, no es acertado decir que estoy intuyendo un ruido. Lo que estoy intuyendo es el teléfono, igual que intuyo el teléfono cuando lo veo o cuando lo toco. Mi entendimiento puede sintetizar en una misma intuición sensaciones de distinta naturaleza. Por eso mismo, si, por ejemplo, siento miedo, no es acertado decir que intuyo miedo, sino más bien que intuyo lo que podemos llamar mi yo intuitivo, de modo que, al igual que al oír el timbre de mi teléfono digo que tengo una intuición de mi teléfono sonando, cuando siento miedo tengo una intuición de "yo asustado". También me estoy intuyendo a mí (como intuición) cuando  tengo conciencia de mis pensamientos, de mis voliciones, etc. Huelga decir que no hay que confundir este "yo" intuitivo con el concepto de "yo" trascendental, ni tampoco con el concepto empírico de mi mente. Volveremos sobre esto más adelante.

A partir de aquí nos centramos en la relación de la intuición con la geometría del espacio y el tiempo, que es el tema principal de esta página. Una de las capacidades de las que nos dota nuestro entendimiento es la posibilidad de describir nuestras intuiciones en términos de conceptos. La conceptualización de una intuición ya no es una intuición, sino un pensamiento. Por ejemplo, no es lo mismo ver (intuir) algo verde que ser consciente de que estamos viendo algo verde y no algo rojo. El hecho es que siempre que vemos algo verde podemos generar el pensamiento "esto es verde". Del mismo modo, cuando vemos o imaginamos una línea, podemos distinguir si es recta o es curva. No podemos definir "recta", igual que no podemos definir "verde". Simplemente, nuestro entendimiento sabe cuándo los conceptos de "recta" o "verde" son adecuados para describir una intuición y cuándo no. El criterio por el que nuestro entendimiento decide si una línea es recta o no (o si un color es verde o no) lo establece a priori, y esto explica que nuestro entendimiento no pueda equivocarse al emitir un juicio de esta clase (salvo por cuestiones de precisión: nuestro entendimiento tomará por recto el horizonte marino, cuando en realidad es un arco de una circunferencia enorme).

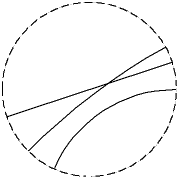Para entender que, realmente, el entendimiento decide a priori llamar rectas a lo que llama rectas, podemos pensar en un ejemplo similar al del Adán que considerábamos en la página anterior. Imaginemos ahora un ser consciente diferente, al que podemos llamar Eva, cuya capacidad de percepción no le muestra un plano infinito, sino únicamente un círculo plano, pero un círculo abierto, lo cual significa que su campo visual no incluye la circunferencia que bordea el círculo. Ahora vamos a suponer algo que ni siquiera Matrix puede lograr, a saber, que el entendimiento de Eva conceptualiza de forma diferente las sensaciones que le llegan. Al igual que nosotros, cuando Eva ve una línea, su entendimiento le dice si es recta o no, pero no lo decide con el mismo criterio que nosotros: Eva "ve" como rectas únicamente aquellas rectas (en el sentido que nosotros damos al término) que pasan por el centro del círculo, así como aquellos arcos de circunferencia que cortan perpendicularmente al círculo exterior (que ella no ve). Por ejemplo, Eva ve rectas las tres líneas que aparecen representadas en la figura. Nosotros vemos que una de ellas es recta, pero las otras dos las vemos curvas. Nuestro entendimiento nos las presenta como curvas, pero nada impide a priori que pueda existir una Eva que, ante estas mismas tres líneas, tenga la intuición de que está viendo tres rectas y, por otra parte, llame curva a una recta (para nosotros) que no pase por el centro del círculo.

Debemos entender bien esto: nosotros no tenemos conciencia de hacer ningún cálculo cuando vemos las tres líneas y decimos que una es recta y las otras dos no. Del mismo modo, Eva ve las tres y dice con la misma inmediatez que las tres son rectas. Más aún, esto significa que Eva no las distingue más que por su posición en el plano, igual que para nosotros dos rectas cualesquiera son iguales salvo por su posición. Eva considerará que cualquiera de las tres rectas puede moverse de forma continua (sin ser deformada) hasta superponerse con cualquiera de las otras dos. Si grabamos en vídeo lo que Eva entiende por un movimiento, a nuestros ojos será una deformación y, recíprocamente, si, por ejemplo, trasladamos el diámetro del círculo paralelamente a sí mismo, Eva dirá que estamos moviendo y deformando a la vez una recta, de modo que las curvas que vamos obteniendo, distintas de la de partida, ya no son rectas. Por otra parte, al igual que nosotros sabemos trazar mentalmente la recta que une dos puntos cualesquiera, también Eva sabe hacer lo mismo, pero su mente dibujará una línea que, en general, nosotros tendremos por curva.

Tal y como decíamos, el hecho de que Eva pueda existir (al menos en teoría) demuestra que la distinción que hacemos entre líneas rectas y curvas no es a posteriori, sino a priori. Yo no "veo" que una línea dada es recta, sino que lo "decido" como parte de los criterios que utilizo para interpretar intuitivamente mis percepciones. En realidad, dicho así, es capcioso: lo que yo decido es el criterio, pero, una vez fijado el criterio, yo ya no puedo decidir si una línea dada es o no recta, será lo que corresponda. Es lo mismo que ya comentábamos sobre los sonidos "Yovi rosas sekas". Si convenimos en interpretarlos como una frase castellana, significa "Yo vi rosas secas", y no puede significar otra cosa, mientras que si convenimos en interpretarlos como una frase latina, entonces significa "Cortas rosas para Júpiter", y no puede significar otra cosa. Yo observo que no tengo otro criterio para interpretar mis percepciones que el dado por la geometría euclídea, llamando rectas a lo que llamo rectas y no a otra cosa. No puedo asegurar a priori que no fuera posible "reeducar" mi mente y hacer que al ver el círculo que ve Eva pudiera reconocer como rectas de forma intuitiva las mismas líneas que Eva reconoce como tales; pero lo cierto es que, hoy por hoy, no puedo.

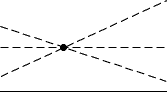Dado que el entendimiento de Eva aplica un criterio diferente, Eva llegará a conclusiones geométricas muy distintas de las nuestras. Por ejemplo, mi intuición me garantiza que por un punto exterior a una recta pasa una única paralela. ¿Cómo sé yo esto? Me imagino una recta y un punto exterior a ella, y enseguida puedo imaginarme una paralela que pasa por ese punto. Más aún, me doy cuenta de que cualquier otra recta que pase por el punto, distinta de la paralela que he imaginado, deberá acercarse hacia la recta dada, sea por un lado, sea por el otro, por lo que acabará encontrándola y no será paralela. Además me doy cuenta de que esto no depende para nada de la recta o el punto elegidos, ya que cualquier otra recta y cualquier otro punto están en las mismas condiciones.

Si el lector reflexiona sobre este "argumento", debería darse cuenta de que "hace aguas" por todas partes, y ello se debe a que no es posible razonar si por un punto exterior a una recta pasa una paralela, muchas o ninguna. A la hora de axiomatizar la geometría euclídea, es necesario tomar como axioma la existencia y unicidad de las paralelas (o alguna afirmación equivalente). La convicción de que, en efecto, el llamado postulado de las paralelas es verdadero, no puede provenir de ningún razonamiento, sino que procede de nuestra intuición. Sabemos que no puede ser falso, no porque no pueda ser falso, que puede serlo, sino porque no puede ser falso siendo nuestra intuición la que es. En el párrafo anterior sólo hemos pretendido indicar qué hemos de imaginar para convencernos de que es cierto, pero sólo obtendremos la conclusión cuando pongamos en juego la intuición.

Muy distinta es la situación para Eva. Si volvemos a las tres "rectas" anteriores, Eva ve que dos de ellas se cortan en un punto, pero ambas son paralelas a la tercera. Así, tenemos una recta y un punto exterior por el que pasan dos paralelas distintas. De hecho, Eva se ve capaz de trazar infinitas paralelas distintas a una recta dada que pasan por un punto exterior dado. El plano que ve Eva es lo que los matemáticos llaman plano de Poincaré, y satisface una geometría similar en lo esencial a la geometría euclídea (es decir, una geometría en la que se puede hablar de rectas, segmentos, ángulos, triángulos, distancias, paralelas, perpendiculares, etc.), pero que se diferencia precisamente en este aspecto: por un punto exterior a una recta pasan infinitas paralelas. Es lo que los matemáticos llaman la geometría hiperbólica.

El hecho de que podamos afirmar con total seguridad el postulado de las paralelas prueba su carácter a priori. Un ejemplo de afirmación a posteriori es que todos los cuerpos caen. (Nos referimos, por precisar, a todos los cuerpos situados en la superficie de la Tierra.) Aunque la ciencia dé esta afirmación por incuestionable, nada me impide imaginar que levanto un bolígrafo a unos centímetros de la mesa, lo dejo en el aire y se queda ahí, sin caer, y sin que ello pueda explicarse en términos de un truco de prestidigitación. Más adelante discutiremos hasta qué punto puedo asegurar que jamás veré algo así, pero en el caso de las paralelas no se plantea un problema similar: el hecho de que "no quepa en mi conciencia" percibir dos paralelas a una recta dada que no sean paralelas entre sí, es razón suficiente para estar seguro de que jamás veré algo así.

Para que tenga sentido decir que sabemos algo a posteriori, es decir, que lo sabemos porque nos lo muestra la experiencia, es imprescindible que la experiencia pudiera también refutarlo. (Por ejemplo, no podemos asegurar a priori que todos los cuerpos caen porque una experiencia podría, en teoría, mostrarnos lo contrario.) Por ello, puesto que es imposible imaginar dos rectas paralelas a una tercera que no sean paralelas entre sí, es imposible a fortiori tener una experiencia que nos muestre algo así, y ello descarta la posibilidad de que el principio de las paralelas sea un conocimiento a posteriori. Por otro lado, el hecho de que esto sí quepa en la conciencia de Eva prueba que el principio de las paralelas no es una identidad lógica, algo que no pudiera haber sido falso.

En resumen, podemos concluir que nuestra intuición nos legitima para hacer afirmaciones geométricas que no son identidades lógicas y que, por consiguiente, sólo podemos afirmarlas en calidad de afirmaciones trascendentales, es decir, afirmaciones que no podemos negar porque nuestra conciencia no puede concebir ninguna alternativa.

El principio de las paralelas es sólo un ejemplo de las muchas afirmaciones geométricas que podemos afirmar sin que medie razonamiento alguno tomando como base nuestro conocimiento trascendental sobre nuestra intuición. Otros ejemplos serían:

• Una circunferencia divide al plano en dos regiones (el interior y el exterior), de modo que dos puntos están en la misma región si podemos pasar (continuamente) de uno a otro sin cruzar la circunferencia.
• Si una recta pasa por un punto interior de una circunferencia, entonces corta a la circunferencia exactamente en dos puntos.
• Si un triángulo tiene un ángulo obtuso, entonces tiene los otros dos ángulos agudos.
  

La geometría euclídea puede ser axiomatizada tomando como axiomas unas pocas de estas afirmaciones, de modo que todas las demás pueden deducirse lógicamente de ellas, aunque para nuestra intuición sean igual de evidentes que las que hemos tomado como axiomas. Por otra parte, a partir de estas afirmaciones geométricas evidentes es posible deducir otras afirmaciones que la intuición ya no puede asegurar de forma inmediata. Por ejemplo: "La suma de los ángulos de un triángulo es igual a un ángulo llano." (Nadie ve un triángulo cualquiera y dice sin más: "es evidente", al contrario de lo que sucede con las tres afirmaciones anteriores.)

Debemos ser prudentes sobre las restricciones que nuestra intuición impone a priori a nuestra experiencia. Es cierto que podemos afirmar a priori que nunca veremos un trozo de queso triangular con dos ángulos obtusos, pero pensemos en lo siguiente: la intuición nos dice que si caminamos en línea recta nos alejamos cada vez más del punto de partida y, en particular, nunca regresaremos a él. Ahora bien, imaginemos que estoy en Matrix y que ésta me muestra un suelo perfectamente plano sobre el cual me hallo, y veo que formo parte de una fila de copias de mí mismo, separadas por unos diez metros de distancia. En realidad no son copias, sino que soy yo mismo, en el sentido de que si, por ejemplo, tiro una pelota "al siguiente" de la fila, la pelota me llega por la espalda o, al revés, si dejo la pelota en el suelo (una pelota única, firmada por mí, con sus manchas particulares, etc.) y me pongo a caminar en línea recta por el suelo plano, al cabo de diez metros me encuentro la pelota, con mi firma y mis propias manchas. En términos matemáticos, en lugar de un espacio euclídeo infinito, Matrix me está mostrando el equivalente tridimensional de una superficie cilíndrica. Las imágenes que veo no son copias de mí mismo, sino que la luz que yo reflejo por detrás "da la vuelta" a la habitación y me llega por delante, y viceversa.

Ante esta tesitura, tendría que plantearme si estoy en un universo infinitamente "autorreplicado" o si, por el contrario, es más razonable asumir que se trata de un universo con una topología diferente a la del espacio euclídeo usual. En cualquier caso, mi intuición no puede concebir que yo camine en línea recta y vuelva al punto de partida (aunque el lugar al que llegue tenga exactamente las mismas características que el que he abandonado), por lo que intuitivamente no tengo más opción que la de la autorreplicación, pero eso no impide que, desde un punto de vista racional, pueda ser más conveniente aceptar que la geometría del universo difiere de la geometría de la intuición. Volveremos sobre esto más adelante, ya que, aunque por motivos diferentes, esto no es especulación pura, sino que sucede así en realidad.

Del mismo modo que mi intuición externa me permite fundamentar la geometría (mejor dicho, una geometría), la intuición interna y la externa me permiten fundamentar la aritmética y otras partes básicas de la matemática. Consideremos por ejemplo estos cinco puntos:

Nuestra intuición nos dice que están alineados. El interpretar como "alineación" a esta configuración es algo que nuestro entendimiento hace a priori. Eva podría ver estos mismos puntos y entender que no están alineados. Es imposible "demostrar" de algún modo que los puntos están alineados. Simplemente, al intuirlos, nuestra intuición entiende que lo están. Del mismo modo, no podemos "demostrar" que en la figura hay precisamente cinco puntos. Es una afirmación tan intuitiva como la referente a la alineación. Ciertamente, podemos contarlos: los recorremos pensado: "uno, dos, tres, cuatro y cinco", pero eso no es un razonamiento. El concepto de "cinco" es un concepto intuitivo igual que lo es el de "recta". Esto significa que es nuestra intuición y no nuestra razón quien nos dice en principio cuándo procede y cuándo no procede aplicarlo para describir una intuición dada. No obstante, esto no excluye que, en un determinado contexto, nuestra razón pueda predecir que el concepto de "cinco" será aplicable. Quizá esto se entienda mejor si lo pensamos con un número más grande: supongamos que vemos una habitación rectangular con el suelo embaldosado y contamos que contra una pared hay 12 baldosas y contra la otra hay 10. Entonces podemos razonar que en total habrá 120 baldosas, sin necesidad de contarlas una a una. Esto es un hecho aritmético análogo al hecho geométrico de que si rompemos un triángulo y ponemos sus ángulos consecutivamente obtendremos un ángulo llano, y sabemos que será así a priori, sin necesidad de hacerlo.

Como en el caso de la geometría, es posible organizar deductivamente la aritmética, de modo que los hechos aritméticos básicos pueden deducirse lógicamente a partir de unos pocos axiomas, axiomas que la intuición nos da por verdaderos. Por ejemplo, uno de estos axiomas podría ser "todo número natural tiene un sucesor", lo cual es una afirmación intuitivamente verdadera sobre los números naturales, ya que mi intuición me dice que si me imagino una cantidad arbitraria de puntos, como los cinco de la figura anterior, siempre puedo imaginarme todos esos puntos y uno más. De entre las consecuencias de esos axiomas, habrá algunas que no sean intuitivamente evidentes y otras que sean tan evidentes como los propios axiomas. Por ejemplo, consideremos la afirmación "el orden de los factores no altera el producto". Aunque un matemático puede demostrarlo, no sin cierta artificiosidad, a partir de hechos aritméticos más simples, para convencernos de la verdad de este hecho basta pensar en una figura como la siguiente:

Vemos que podemos concluir que consta de 15 puntos bien contando que tiene 3 veces 5 puntos o bien contando que tiene 5 veces 3 puntos. Además nos damos cuenta de que podemos construir un rectángulo análogo cuyos lados contengan cualquier par de números prefijados, por lo que el orden de los factores es irrelevante, no sólo en el producto 3 x 5 = 5 x 3, sino en cualquier otro producto. Como en el caso de nuestra "demostración" del postulado de las paralelas, lo que acabamos de decir no es válido como razonamiento lógico. El "nos damos cuenta de que" no es un argumento racional, sino una llamada a la intuición, que es capaz de darnos una respuesta de la que podemos estar absolutamente seguros, ya que no estamos hablando de cualquier cosa, sino de qué somos capaces y qué no somos capaces de concebir, y sobre eso tenemos necesariamente cierta cualificación para pronunciarnos.

Llamaremos intuición pura a la intuición en su uso estrictamente formal, es decir, cuando la usamos para determinar a priori qué podemos y qué no podemos intuir, sin aplicarla con ello a la interpretación de ninguna percepción particular. En estos términos, podemos decir que la intuición pura sirve de fundamento a una parte de la matemática pura, la parte que estudia aquellos conceptos que tienen una interpretación intuitiva. Esto incluye a la geometría euclídea, la aritmética de los números naturales, enteros y racionales y, en general, toda la matemática llamada finitista, es decir, que involucra exclusivamente conjuntos finitos. Hasta cierto punto, la intuición nos permite también dar sentido y, en algunos casos, asegurar ciertas afirmaciones que involucran conjuntos numerables, como el propio conjunto de los números naturales, si bien discutir esto aquí nos alejaría demasiado del propósito de estas páginas.

Para el resto de las matemáticas no disponemos de otra fundamentación que no sea una teoría axiomática adecuada. Algunos matemáticos identifican axiomatización con rigor, de modo que desprecian los argumentos intuitivos por imprecisos y engañosos. Paradójicamente, nadie puede defender las teorías axiomáticas como única forma de razonamiento matemático válido sin desconocer qué es con detalle una teoría axiomática, dado que para dar rigor al concepto de teoría axiomática es imprescindible tratar intuitivamente con algunos conceptos finitistas, tales como "signos", "cadenas de signos", "conjuntos de cadenas de signos", "números naturales", etc. Resulta, pues, que toda la matemática descansa en último término sobre las afirmaciones que podemos garantizar intuitivamente, sea de forma directa, cuando usamos la intuición como fuente de premisas válidas para razonar a partir de ellas, sea de forma indirecta, cuando usamos la intuición para definir teorías axiomáticas y determinar los procedimientos admisibles para operar con ellas, como único medio para razonar sobre conceptos sin un contenido intuitivo exacto.

Con lo de "contenido intuitivo exacto" queremos decir que, por ejemplo, el concepto de "función real de variable real" tiene parcialmente un contenido intuitivo, en el sentido de que podemos representar gráficamente algunas funciones de manera que, viendo la gráfica, podemos predecir algunos hechos sobre las mismas demostrables en el seno de una teoría axiomática, pero no hemos de olvidar que el concepto de "función" es mucho más amplio que el concepto intuitivo de "gráfica", de modo que hay funciones extrañas (como una función continua no derivable en ningún punto) sobre las que no tenemos ninguna imagen intuitiva. Por ello no podemos confiar en la intuición a la hora de hacer afirmaciones generales sobre las funciones reales de variable real. Han sido precisamente estos intentos de usar la intuición para sacar conclusiones que involucran conceptos que son más generales que sus presuntos contenidos intuitivos los que han hecho recelar de la intuición injusta e incoherentemente a muchos matemáticos modernos.

Determinar los límites legítimos de la intuición a la hora de fundamentar la matemática sería una delicada tarea en la que no vamos a entrar, aunque haremos una última observación general: alguien podría argumentar que, al igual que hemos dicho que no poseemos un concepto intuitivo que se ajuste al concepto general, conjuntista, de función real de variable real, tampoco tenemos un concepto intuitivo sobre el número 10¹⁰⁰⁰, ni en particular sobre un polígono regular de 10¹⁰⁰⁰ lados, por lo que, por ejemplo, cuando antes hemos asegurado intuitivamente que el orden de los factores no altera el producto, deberíamos haber precisado que esto sólo es válido para aquellos números de los que pueda formarme una imagen intuitiva, y lo mismo sucedería con cualquier afirmación que justifique intuitivamente sobre polígonos regulares. Sin embargo, esto es falaz y, en el fondo, no es sino una forma de escepticismo. En el sentido habitual, un escéptico es alguien que a priori se niega a usar su razón, y ahora estamos hablando de alguien que, a priori, se niega a aceptar las afirmaciones trascendentales avaladas por la intuición. A este respecto, debemos tener presente que la intuición pura no es un inventario de afirmaciones intuitivas, sino un sistema de criterios generales fijados a priori por mi entendimiento.

Por ejemplo, según una de las reglas aceptadas por la Federación Internacional de Ajedrez, una partida acaba en tablas si se han producido cincuenta movimientos de ambos jugadores sin que se mueva ningún peón y sin que se haya realizado ninguna captura. Por consiguiente, el conocimiento del reglamento del ajedrez nos permite concluir categóricamente que toda partida de ajedrez termina en un tiempo finito. En efecto, cada cincuenta movimientos ha de capturarse al menos una pieza o moverse un peón, pero el número de capturas posibles es finito (porque el número de piezas lo es), y de las reglas que rigen el movimiento de los peones se sigue que cada uno de ellos puede moverse a lo sumo seis veces, luego el número de movimientos de peones en una partida es también finito. Si sumamos las casillas que tiene por delante cada peón en una posición dada, le sumamos el número de piezas (distintas de los reyes) que hay sobre el tablero y multiplicamos el resultado por 50, obtenemos el máximo número de jugadas (dobles) que puede durar la partida a partir de ese momento. Alguien que, pese a este argumento, especulara sobre la posibilidad de que una partida se pueda prolongar indefinidamente se estaría declarando escéptico con ello.

Del mismo modo, yo sé lo que hago a la hora, por ejemplo, de contar intuitivamente los puntos de un rectángulo de puntos mediante una multiplicación, y sé que el proceso es aplicable independientemente del número de puntos que tenga el rectángulo. Por eso puedo asegurar que la independencia del orden de los factores no depende a su vez de su magnitud. El análisis de un criterio puede proporcionar resultados generales a priori sobre los resultados que podemos obtener al aplicarlo, y eso es lo que sucede cuando hacemos afirmaciones trascendentales basadas en nuestra intuición.

Para terminar vamos a abordar frontalmente una pregunta que ya está respondida casi completamente de forma implícita en lo que hemos dicho hasta ahora, pero sobre la que todavía podemos añadir alguna observación adicional: ¿qué son, en definitiva, el espacio y el tiempo?

Según hemos visto, el espacio y el tiempo son la gramática de nuestra intuición. Decir que todas mis intuiciones han de estar necesariamente en el tiempo es como decir que toda palabra que yo pueda entender ha de formar parte de una frase. Las distintas geometrías son como distintas gramáticas de distintos idiomas, de entre las cuales mi intuición sólo es capaz de manejar una. Las demás son como "lenguas muertas", que puedo traducir, pero no hablar de forma natural. Sin embargo, esta analogía se rompe cuando observamos que nuestra conciencia puede recibir intuiciones formales, sin ningún contenido sensible, como cuando imaginamos una recta, o un cubo. Hasta aquí todavía podríamos preservar la analogía comparando un cubo trazado en mi imaginación con una frase como "agiliscosos giroscaban los limazones", arriesgada traducción de un famoso poema de Lewis Carroll. Esta frase no significa nada, si bien en ella podemos determinar relaciones morfosintácticas precisas: giroscaban es un verbo en tercera persona del plural del pretérito imperfecto de indicativo, limazones es un sustantivo masculino plural, que sintácticamente ejerce de sujeto, etc. Pero en el caso de la intuición podemos ir más lejos, ya que podemos intuir un espacio y un tiempo vacíos. Podemos decir que "vemos" el espacio y que "percibimos" el paso del tiempo, lo que, en el caso del lenguaje, sería como leer una frase que no constara de palabra alguna.

Esto se debe a que mi intuición puede proporcionarme información, no sólo sobre una intuición posible en particular, sino sobre todas las intuiciones posibles de una cierta gama. Ya hemos visto un ejemplo al considerar el postulado de las paralelas: yo sé que por un punto exterior a una recta sólo pasa una paralela porque mi intuición me muestra todas las posibilidades de intuir una recta que pase por un punto dado, y ello me permite "ver" que sólo una puede ser paralela a una recta dada. Del mismo modo, cuando veo un objeto ante mí y "veo" que hay un espacio intermedio que me separa de él, lo que estoy "viendo" es que, por ejemplo, mi intuición puede trazar la trayectoria de un objeto puntual que se moviera desde el objeto hasta mí. Cuando "percibo" que pasa el tiempo, no estoy percibiendo nada en realidad; simplemente, lo que sucede es que mi intuición puede imaginar, por ejemplo, el tic-tac de un reloj, es decir, sucesos que podrían ocurrir en distintos instantes, aunque no suceda nada de hecho. "Percibir" el espacio y el tiempo no es sino tener conciencia de la posibilidad de intuir cualquier cosa en distintos lugares y momentos.

Imaginemos que estamos ante una hoja de papel en la que hay dibujado un paisaje en perspectiva. Podemos decir: vemos un camino, que conduce a una casa, detrás de la cual hay unos árboles, tras los cuales se ve una montaña, encima de la cual está el Sol, etc. Supongamos ahora que borramos la casa. Podríamos decir, ahí había una casa, pero ya no está. Si, paulatinamente, vamos borrando cada elemento del paisaje, al final tendríamos una hoja en blanco, pero podríamos seguir viéndola como el paisaje original y decir: ahí había una casa, pero ya no está, como también han quitado los árboles, y las montañas, y el suelo, y el Sol, etc. Pero no es lo mismo ver una hoja de papel y pensarla como una superficie plana que pensarla como una "ventana" a un paisaje tridimensional en el que no hay nada, lo cual no me impide hablar de lo que había o podría haber aquí cerca, y más lejos, etc. Cuando lo pienso así, en realidad no es que esté pensando, sino que estoy intuyendo el espacio tridimensional euclídeo, que es el único que mi entendimiento sabe hacerme intuir. Ante la misma hoja de papel, nuestros Adán y Eva tendrían intuiciones formales distintas, porque lo que intuimos cuando pensamos en un espacio o un tiempo vacíos no está contenido en nuestras percepciones (ya que no tenemos ninguna, o bien estamos haciendo abstracción de ellas), sino que está únicamente en nuestra conciencia. Ya hemos expresado esto diciendo que el espacio y el tiempo (intuitivos) son trascendentalmente ideales.

En particular, aunque existiera una realidad trascendente externa a nuestra conciencia, de modo que los fenómenos que percibimos estuvieran causados por ella, no podríamos asegurar que los objetos de dicha realidad estuvieran situados en un espacio y un tiempo trascendentes. Podría ocurrir que no mantuvieran relaciones espacio-temporales de ninguna clase, o también que estuvieran situados en un espacio y un tiempo trascendentes distintos del espacio y el tiempo intuitivos en los que nuestro entendimiento sitúa a priori los fenómenos. "Ahí fuera" podría haber una realidad espacio-temporal no euclídea, sin que ello contradiga el hecho de que el espacio y el tiempo intuitivos son euclídeos. Más adelante volveremos sobre esto.

Observemos que para que Matrix funcione hemos de conectarlo a un ser consciente que tenga de por sí la capacidad de intuir el espacio y el tiempo (o, al menos, que tenga la capacidad de desarrollar a priori dicha intuición estimulado por las percepciones que Matrix le pueda generar), de tal forma que Matrix no tiene que hacer nada para que su inquilino vea el espacio y el tiempo, sólo tiene que tener asignada una posición en el espacio y en el tiempo para cada suceso que pretenda mostrarle a su inquilino, así como la posición espacio-temporal de éste, y calcular qué percepciones corresponden al suceso en función de dichas posiciones. Será la mente del inquilino la que deberá reconstruir a partir de dichas percepciones las relaciones espacio-temporales oportunas, Matrix no puede dárselas. Aunque Matrix no aporte ninguna sensación al inquilino, éste seguirá intuyendo el espacio vacío a su alrededor, así como el paso del tiempo, porque estas intuiciones no proceden de Matrix, sino de su propio entendimiento. Hablamos de un Matrix normal, porque nuestro Adán no entendería eso de "espacio a su alrededor". Él, en caso de no ver nada, seguiría teniendo la intuición formal de su plano vacío. Un plano en el que él mismo no tiene cabida.

Esto debería bastar para que el lector se convenza de que el espacio y el tiempo intuitivos no son nada misterioso (salvo que considere misterioso el hecho mismo de que tengamos intuiciones, de lo cual hemos de hablar más adelante). El espacio y el tiempo están en nuestras intuiciones (o viceversa) en el mismo sentido en que la gramática está en todas las frases que entendemos. Decir que "esto está delante de aquello" es como decir que "este adjetivo determina a aquel sustantivo".