Figures convexes
Una figura és convexa quan el segment que determinen un parell qualsevol de punts que pertanyen a eixa figura està contingut dintre de la pròpia figura. La lluna plena, per exemple, és convexa; el el quart creixent no ho és:
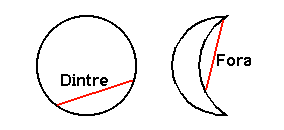
El cercle és una figura convexa i el quart creixent no
En 1942, Fu Traing Wang y Chuan-Chih Hsiung, de la Universitat Nacional de Chekíang, demostraren que en el tangram només es poden construir 13 figures convexes (American Mathematical Monthly, vol. 49) les quals es proposen al final del text.
Qualsevol figura composta por las peces del tangram es pot dividir en 16 triangles isòsceles de angle recte (triangles bàsics).
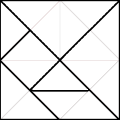
Descomposició en triangles bàsics
Anomenarem costats racionals als dos costats més curts i costat irracional al més llarg.
En aquestes condicions, Fu Traing Wang y Chuan-Chih Hsiung argumentaren de la següent manera:
Qualsevol polígon convex format amb les peces del tangram acompleix que cada costat racional de qualsevol triangle bàsic que el composa està a sobre de un costat racional d'altre triangle bàsic o pertany al perímetre del polígon (i el mateix per als costats irracionals).
Totes les peces del tangram són
-
Triangles els costats racionals (del mateix tipus) del qual formen un angle recte i els de tipus diferents formen angles aguts.
-
Un quadrat amb els quatre costat racional (del mateix tipus) els quals formen angles rectes
-
Un romboide els angles del qual són aguts i obtusos de forma alterna i els costats del qual són racionals i irracionals també de forma alterna.
Anomenarem costats racionals del polígon convex als formats per costats racionals dels triangles bàsics i irracionals als formats per costats irracionals. Aleshores, dos costats consecutius són del mateix tipus (racionals o irracionals) quan formen un angle recte (90º = 45º + 45º), y diferents quan formen un angle agut (45º) o obtús (135º = 90º + 45º = 45º + 45º + 45º).
Si designem n al nombre d'angles , per tant, també de costats del polígon, p al nombre d'angles aguts, q al nombre d'angles rectes i r al nombre d'angles obtusos tenim què
p + q + r = n
Com la suma de tots los angles d'un polígon convex de n costats és igual a
(n – 2)·180º
tenim què
45·p + 90·q + 135·r = (n – 2)·180º
i si eliminem r ens resulta què
2·p + q = 8 – n
Com p i q tenen que ser iguals o majors que
zero, el polígon podrà tindre com a màxim huit costats i, clar està, com a
mínim tres. A més, els valors de p, q, r i n, es limiten a un nombre reduït de
possibilitats què hem obtingut amb l'ajuda d'un 
programa
en llenguatge C i que presentem en la llista següent:
-
huit costats amb huit angles obtusos
-
set costats amb un angles recte i sis obtusos
-
sis costats amb dos angles rectes i quatre obtusos
-
sis costats amb un angles agut i cinc obtusos
-
cinc costats amb tres angles rectes i dos obtusos
-
cinc costats amb un angles recte, un agut i tres obtusos
-
quatre costats amb quatre angles rectes
-
quatre costats amb dos angles aguts i dos obtusos
-
quatre costats amb dos angles rectes, un agut i un obtús i
-
tres costats con un angles recte y dos aguts
Si en cada cas tenim en compte el nombre de costats i el nombre d'angles y que no són rectes, observem que en cap polígon convex tindrem més de quatre costats irracionals.
Per tant, podem inscriure qualsevol d'aquestos polígons convexos dintre d'un rectangle (PQRS), de forma que els costats racionals del polígon ABCDEFGH coincideixen amb els costats del rectangle (si tots els costats del polígon són irracionals aleshores el polígon i el rectangle només tenen en comú els vèrtex del primer).
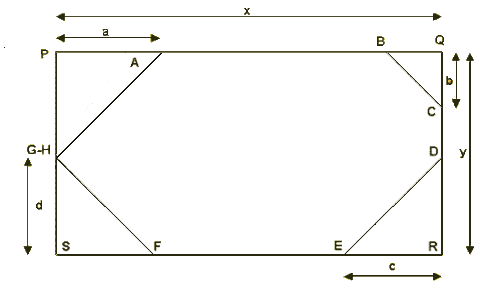
El polígon convex ABCDEFGH inscrit en el rectangle PQRS
Si suposem que la longitud del costat PQ és igual a x vegades la longitud del costat racional del triangle bàsic i que per al costat PS és igual a y vegades, tindrem que l'àrea del rectangle PQRS és igual l'àrea del triangle bàsic multiplicada per 2xy.
Si els costats irracionals (HA, BC, DE y FG) del polígon convex tenen una longitud igual a la longitud del costat irracional del triangle bàsic multiplicada por a, b, c i d respectivament (amb la possibilitat de que a, b, c o d pdoen valer zero), tindrem que l'àrea dels triangles PAH, BQC, DRE i FSG és igual a les àrees dels triangles bàsics multiplicades per a2, b2, c2 i d2 respectivament.
Com el polígon està composat per 16 triangles bàsics, es dedueix que
a2
+ b2
+ c2 + d2 = 2xy – 16,
quan a + b £ x, c + d £
x, a + d £ y, b + c £
y.
Amb les solucions senceres no negatives d'aquesta equació resolem el problema original.
Per a acotar el problema podem suposar que la base del rectangle PQRS és major que la altura, és a dir, x ³ y. També podem suposar que 0 < x £ 16 perquè aquestos són els casos extrems (que no s'abasten) corresponents a que la base del rectangle PQRS està formada des de 1 triangle bàsic fins els 16 triangles bàsics.
Hem obtingut les soluciones senceres i no negatives
per a l'equació anterior amb la ajuda d'un programa en
llenguatge C i després d'eliminar les solucions corresponents a rotacions
i simetries de polígons iguales, les presentem en la taula:
|
x |
y |
a |
b |
c |
d |
Polígon número |
|
x = 3 |
y = 3 |
a = 0 |
b = 1 |
c = 0 |
d = 1 |
1 |
|
x = 3 |
y = 3 |
a = 1 |
b = 0 |
c = 0 |
d = 1 |
2 |
|
x = 4 |
y = 2 |
a = 0 |
b = 0 |
c = 0 |
d = 0 |
3 |
|
x = 4 |
y = 3 |
a = 0 |
b = 0 |
c = 2 |
d = 2 |
4 |
|
x = 4 |
y = 3 |
a = 2 |
b = 0 |
c = 2 |
d = 0 |
5 |
|
x = 4 |
y = 4 |
a = 0 |
b = 4 |
c = 0 |
d = 0 |
6 |
|
x = 4 |
y = 4 |
a = 2 |
b = 2 |
c = 2 |
d = 2 |
7 |
|
x = 5 |
y = 2 |
a = 0 |
b = 0 |
c = 0 |
d = 2 |
8 |
|
x = 5 |
y = 2 |
a = 1 |
b =1 |
c =1 |
d = 1 |
9 |
|
x = 5 |
y = 3 |
a = 0 |
b = 1 |
c = 2 |
d = 3 |
10 |
|
x = 5 |
y = 3 |
a = 0 |
b = 2 |
c = 1 |
d = 3 |
11 |
|
x = 5 |
y = 5 |
a = 0 |
b = 5 |
c = 0 |
d = 3 |
No es pot construir |
|
x = 5 |
y = 5 |
a = 1 |
b = 4 |
c = 1 |
d = 4 |
No es pot construir |
|
x = 6 |
y = 2 |
a = 0 |
b = 0 |
c = 2 |
d = 2 |
12 |
x = 6 |
y = 2 |
a = 0 |
b = 2 |
c = 0 |
d = 2 |
13 |
|
x = 6 |
y = 4 |
a = 4 |
b = 0 |
c = 4 |
d = 0 |
No es pot construir |
|
x = 9 |
y = 8 |
a = 8 |
b = 0 |
c = 8 |
d = 0 |
No es pot construir |
