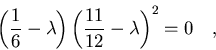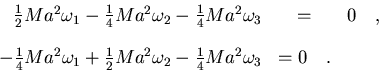

Next: About this document ...
Up: El sólido rígido
Previous: Energía cinética de rotación
Estudiemos con un poco más de detalle el tensor que acabamos de
introducir,  ,
con componentes Iij.
Si suponemos, como anteriormente, que
,
con componentes Iij.
Si suponemos, como anteriormente, que
tendremos
Si
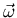 está dirigido a lo largo del eje y,
está dirigido a lo largo del eje y,
Por último, si
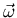 está dirigido a lo largo del eje x,
está dirigido a lo largo del eje x,
Examinando estas ecuaciones, vemos quién tiene la culpa de que 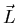 no sea paralelo a
no sea paralelo a
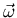 :
los elementos no diagonales del tensor
de inercia. Si
:
los elementos no diagonales del tensor
de inercia. Si
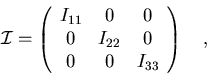 |
(7.30) |
y
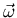 está dirigido a lo largo del eje x, y o z (a
los
que llamaremos ejes principales de inercia), entonces
está dirigido a lo largo del eje x, y o z (a
los
que llamaremos ejes principales de inercia), entonces
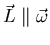 .
La pregunta que nos hacemos es, por tanto, ¿Es posible
encontrar un sistema de ejes (un sistema de referencia) en el que
.
La pregunta que nos hacemos es, por tanto, ¿Es posible
encontrar un sistema de ejes (un sistema de referencia) en el que 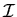 sea diagonal? La respuesta es: sí, ya que toda matriz
simétrica
puede diagonalizarse y además puede demostrarse (ver Apéndice A) que sus
autovalores son reales. Sus autovalores serán I11, I22 e
I33, que abreviadamente suelen escribirse I1, I2 e I3. Los
autovectores serán los ejes respecto de los cuales
sea diagonal? La respuesta es: sí, ya que toda matriz
simétrica
puede diagonalizarse y además puede demostrarse (ver Apéndice A) que sus
autovalores son reales. Sus autovalores serán I11, I22 e
I33, que abreviadamente suelen escribirse I1, I2 e I3. Los
autovectores serán los ejes respecto de los cuales 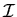 es
diagonal.
Veamos cómo plantear el problema matemático.
Partamos de un sistema de referencia en el cual
es
diagonal.
Veamos cómo plantear el problema matemático.
Partamos de un sistema de referencia en el cual 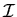 no es
diagonal. Tendremos entonces
no es
diagonal. Tendremos entonces
Sabemos que existen tres ejes respecto de los cuales
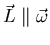 .
Supongamos que
.
Supongamos que 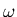 está dirigida justamente a lo
largo
de uno de esos ejes. Tendremos que, además de la ecuación anterior, se
satisface
está dirigida justamente a lo
largo
de uno de esos ejes. Tendremos que, además de la ecuación anterior, se
satisface
donde I es uno de los momentos principales de inercia. Es decir,
tendremos que
Restando ambos términos de la igualdad,
o, en forma matricial,
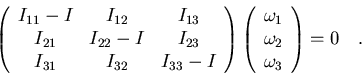 |
(7.31) |
Lo que hemos planteado en definitiva es un sistema de ecuaciones
homogéneo, donde las incógnitas son 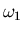 ,
,
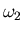 y
y 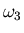 .
Puesto que el sistema es homogéneo, sólo tendrá solución no trivial si
el determinante de los coeficientes es nulo:
.
Puesto que el sistema es homogéneo, sólo tendrá solución no trivial si
el determinante de los coeficientes es nulo:
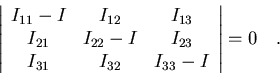 |
(7.32) |
Esto es una ecuación de tercer orden en I que nos proporcionar tres
valores de I (I1, I2 e I3) a lo largo de las direcciones
principales, es decir, los tres autovalores. Los autovectores serán
tres conjuntos de valores
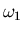 ,
,
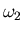 y
y 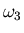 que sólo podrán obtenerse
salvo una
constante (al tratarse de un sistema homogéneo con solución no trivial,
una de las ecuaciones debe ser combinación lineal de las otras dos, es
decir, no podemos obtener el conjunto de valores
que sólo podrán obtenerse
salvo una
constante (al tratarse de un sistema homogéneo con solución no trivial,
una de las ecuaciones debe ser combinación lineal de las otras dos, es
decir, no podemos obtener el conjunto de valores 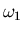 ,
,
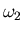 y
y 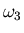 en forma absoluta, sino sólo
dos componentes en función de una tercera, o lo que es lo mismo, sólo
pueden obtenerse las direcciones correspondientes a las velocidades
angulares de giro, pero no los valores de las velocidades).
Hagamos un ejemplo de cálculo del tensor de inercia y de determinación
del sistema de ejes principales.
Lo que nos interesa determinar es el tensor de inercia respecto de un
cierto sistema de referencia por el que se supone pasará el eje de
giro y por tanto será un punto fijo en el sólido. En ese
sentido, ya que no nos interesa el estudio del movimiento de
traslación del sólido, sino sólo el de rotació, por
simplicidad matemática vamos a elegir un sistema de referencia cuyo
origen no es el centro de masas del sólido.
Tomemos como ejemplo el caso de un cubo de densidad de mas homogénea
en forma absoluta, sino sólo
dos componentes en función de una tercera, o lo que es lo mismo, sólo
pueden obtenerse las direcciones correspondientes a las velocidades
angulares de giro, pero no los valores de las velocidades).
Hagamos un ejemplo de cálculo del tensor de inercia y de determinación
del sistema de ejes principales.
Lo que nos interesa determinar es el tensor de inercia respecto de un
cierto sistema de referencia por el que se supone pasará el eje de
giro y por tanto será un punto fijo en el sólido. En ese
sentido, ya que no nos interesa el estudio del movimiento de
traslación del sólido, sino sólo el de rotació, por
simplicidad matemática vamos a elegir un sistema de referencia cuyo
origen no es el centro de masas del sólido.
Tomemos como ejemplo el caso de un cubo de densidad de mas homogénea
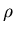 y de lado a, con tres aristas sobre los ejes x, y y z.
Llamemos como siempre x1, x2 y x3 a las coordenadas.
Puesto que el cubo presenta simetría respecto de los ejes 1, 2 y 3,
vemos que es suficiente calcular I11 e I12, ya que, por
simetría
y de lado a, con tres aristas sobre los ejes x, y y z.
Llamemos como siempre x1, x2 y x3 a las coordenadas.
Puesto que el cubo presenta simetría respecto de los ejes 1, 2 y 3,
vemos que es suficiente calcular I11 e I12, ya que, por
simetría
e
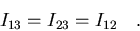 |
(7.34) |
Tendremos por tanto:
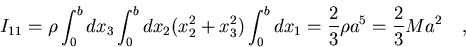 |
(7.35) |
donde M es la masa del cubo.
La componente no diagonal vale:
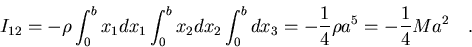 |
(7.36) |
Por lo tanto
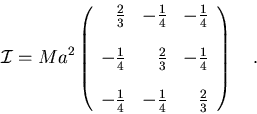 |
(7.37) |
Si
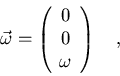 |
(7.38) |
tendremos
![\begin{displaymath}\vec L=\left(
\begin{array}{r}
-\frac{1}{4}\\ [12pt]
-\fra...
...\\ [12pt]
\frac{2}{3}
\end{array}
\right)Ma^2\omega\quad ,
\end{displaymath}](img85.gif) |
(7.39) |
luego 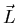 no es paralelo a
no es paralelo a 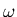 ,
es decir, el sistema de
referencia en el que hemos hallado el tensor de inercia no es el sistema
principal de ejes. Para hallar el sistema de ejes principales, como
hemos comentado anteriormente, hemos de plantear la ecuación:
,
es decir, el sistema de
referencia en el que hemos hallado el tensor de inercia no es el sistema
principal de ejes. Para hallar el sistema de ejes principales, como
hemos comentado anteriormente, hemos de plantear la ecuación:
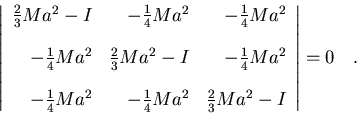 |
(7.40) |
Dividiendo por Ma2 y llamando
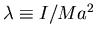 ,
podemos
reescribir el determinante anterior como:
,
podemos
reescribir el determinante anterior como:
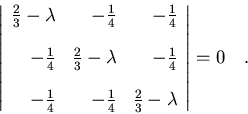 |
(7.41) |
Sumando las columnas 2 y 3 a la 1,
![\begin{displaymath}\left\vert
\begin{array}{rrr}
\frac{1}{6}-\lambda & -\frac{...
...rac{2}{3}-\lambda\\ [12pt]
\end{array}
\right\vert=0\quad ,
\end{displaymath}](img89.gif) |
(7.42) |
luego
![\begin{displaymath}\left(\frac{1}{6}-\lambda\right)
\left\vert
\begin{array}{r...
...rac{2}{3}-\lambda\\ [12pt]
\end{array}
\right\vert=0\quad .
\end{displaymath}](img90.gif) |
(7.43) |
Restando la primera fila en la segunda y tercera,
![\begin{displaymath}\left(\frac{1}{6}-\lambda\right)
\left\vert
\begin{array}{r...
...c{11}{12}-\lambda\\ [12pt]
\end{array}
\right\vert=0\quad .
\end{displaymath}](img91.gif) |
(7.44) |
En forma de ecuación,
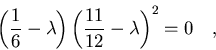 |
(7.45) |
luego los tres autovalores son:
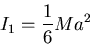 |
(7.46) |
e
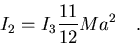 |
(7.47) |
Para determinar la dirección de los ejes de simetria hemos de volver
a las ecuaciones planteadas, pero sólo hemos de trabajar con dos ya
que la tercera es una combinación lineal de las otras dos. De otra
forma, la solución del sistema de ecuaciones homogéneo
sería la trivial. Planteemos dos ecuaciones sustituyendo I por
Ma2/6:
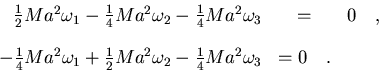 |
(7.48) |


Next: About this document ...
Up: El sólido rígido
Previous: Energía cinética de rotación
Andres Cantarero
1998-12-06
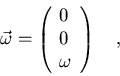
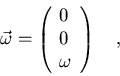
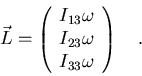
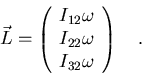
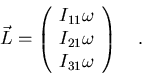
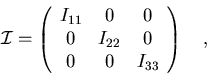
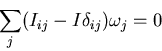
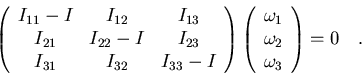
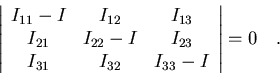
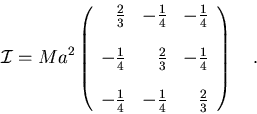
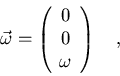
![\begin{displaymath}\vec L=\left(
\begin{array}{r}
-\frac{1}{4}\\ [12pt]
-\fra...
...\\ [12pt]
\frac{2}{3}
\end{array}
\right)Ma^2\omega\quad ,
\end{displaymath}](img85.gif)
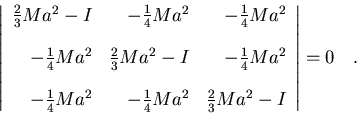
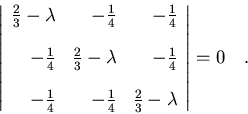
![\begin{displaymath}\left\vert
\begin{array}{rrr}
\frac{1}{6}-\lambda & -\frac{...
...rac{2}{3}-\lambda\\ [12pt]
\end{array}
\right\vert=0\quad ,
\end{displaymath}](img89.gif)
![\begin{displaymath}\left(\frac{1}{6}-\lambda\right)
\left\vert
\begin{array}{r...
...rac{2}{3}-\lambda\\ [12pt]
\end{array}
\right\vert=0\quad .
\end{displaymath}](img90.gif)
![\begin{displaymath}\left(\frac{1}{6}-\lambda\right)
\left\vert
\begin{array}{r...
...c{11}{12}-\lambda\\ [12pt]
\end{array}
\right\vert=0\quad .
\end{displaymath}](img91.gif)