Nonlinear correlation based on binary decompositions
Image decomposition is widely applied in many areas of image processing, for example subband
decomposition. Examples of binary decomposition are threshold decomposition, bitmap
decomposition, and the sliced orthogonal nonlinear generalized (SONG) decomposition. Our
motivation for using binary decompositions is the possibility to optically implement those
correlations with fast spatial light modulators that works in the binary regime.
Threshold decomposition is defined as
 where where 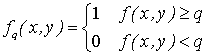
Next figure illustrates a threshold decomposition of a 0-255 gray-scale object.

A two-dimensional image with discrete gray levels can also be decomposed into a sum of
disjoint elementary images eq(f(x,y)) defined as

The SONG decomposition of f(x,y) is
 where where 

Correlation is frequently used of pattern recognition, however other nonlinear
correlation based on binary decompositions are shown to have higher discrimination
capabilities and noise robustness than common linear correlation.
Morphological correlation (MC) is defined as

where gq(x,y) and fq(x,y) are binary versions
of g and f resulting from a threshold decomposition.
We defined the SONG correlation as the summation of multiple linear correlations between
the binary slices of the two functions, g and f, weighting the correlation terms with a weight
coefficient, Wij

At the origin, the autocorrelation sum for all the gray levels yields the total number of
pixels in the objects. In early works on the SONG correlation we set Wij = ð
ij, giving the same weight to all of the gray levels as
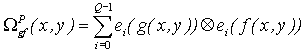
In this expression only the gray levels having the same values for the two images are
correlated together after having their values set equal to one. The SONG correlation is very
discriminating since it counts the number of points in the reference object and in the
reference object and in the image that have the same gray levels at the same locations.
To show the noise robustness of SONG correlation we used images that are degraded by
substitutive noise. We have shown in our papers that SONG correlation is optimum in the
maximum likelihood sense when the image is corrupted by a certain kind of substitutive noise.

Figure: (a) Input scene with the reference object below, and another object to be rejected.
(b) Corrupted image with a high level of substitutive noise.

SEQUENTIAL JOINT TRANSFORM CORRELATOR
The nonlinear correlations that we are studying here are based on a sum of linear
correlation between binary subimages of the targets and of the reference. The sums are
performed on the joint power spectrum (JPS), which is the actual intensity output detected
in the intermediate step of the JTC as
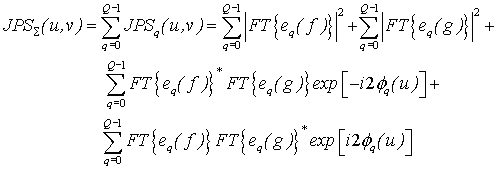
The setup is given by

The rotation and scale changes in the reference objects have been extensive tackled in
pattern recognition. Some of the most effective methods for pattern recognition with in-plane
rotations are based on the circular harmonic and the radial harmonic expansion for scale
invariance.
We have defined the rotation invariant SONGC (RISONGC) as
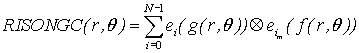
where  is the circular harmonic component (CHC) of the
different binary slices of the reference object and is the circular harmonic component (CHC) of the
different binary slices of the reference object and  are the polar coordinates.
are the polar coordinates.
We present some computer results to determine the performance of the method for rotation
invariant pattern recognition when the input scene is corrupted with substitutive Gaussian
noise





PAPERS ON THE SUBJECT:
- P. García-Martínez and H. H. Arsenault, "A correlation matrix representation using sliced orthogonal nonlinear generalized decomposition," Opt. Commun. 174, 503-515, (2000).
- P. García-Martínez, D. Mas, J. Garcia and C. Ferreira, "Nonlinear morphological correlation: optoelectronic implementation," Appl. Opt. 37, 2112-2118, (1998).
- A. Shemer, D. Mendlovic, G. Shabtay, P. García-Martínez, and J. García, "Modified morphological correlation based on Bit Map representation," Appl. Opt. 38, 781-787 (1999).
- P. García-Martínez, C. Ferreira and D. Mendlovic, "Optical nonlinear correlation based on non uniform subband decomposition," J. Opt & Pure and Appl. Opt. 1, 719-724 (1999).
- A. Fares, P. García-Martínez, C. Ferreira, M. Hamdi and A. Bouzid, "Multichannel chromatic transformation for nonlinear pattern recognition," Opt. Commun. 203, 255-261 (2002).
- P. Garcia-Martinez, Ph. Refregier, H. H. Arsenault and C. Ferreira, "Maximum likelihood for target location in the presence of substitutive noise", Appl. Opt. 40, 3855-3860 (2001).
- M. Tejera, P. García-Martínez, C. Ferreira, D. Lefebvre and H. H. Arsenault, Weighted nonlinear correlation for controlled discrimination capability, Opt. Commun. 201, 29-37 (2002).
- P. García-Martínez, M. Tejera, C. Ferreira, D. Lefebvre and H. H. Arsenault, "Optical implementation of the weighted sliced nonlinear generalized correlation under non-uniform illumination conditions," Appl. Opt. 6867-6874 (2002).
- P. García-Martínez, H. H. Arsenault and C. Ferreira, "Improved rotation invariant pattern recognition using circular harmonic of binary gray level slices", Opt. Commun. 185, 41-48 (2000).
- P. García-Martínez, and H. H. Arsenault, "Nonlinear radial-harmonic correlation using binary decomposition for scale-invariant pattern recognition," Opt. Commun. 223, 255-261 (2003).
- P. Garcia-Martínez, J. Otón, José J. Vallés and H. H. Arsenault, "Nonlinear pattern recognition correlators based on color-encoding single channel systems," Appl. Opt. 42, 425-432 (2004).
- J. Otón, P. García-Martínez, I. Moreno and J. García, "Phase joint transform sequential correlator for nonlinear binary correlations," Opt. Commun. 245, 113-124 (2005).
- C. Ferreira, J. García, P. García-Martínez, H. H. Arsenault, J. J. Esteve-Taboada and J. J. Vallés, "Correlaciones para el reconocimiento de imágenes de intensidad (2D) y de rango (3D)," Opt. Pura y Aplicada 38, 21-33 (2005).
|












 where
where 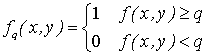

 where
where 
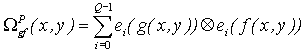
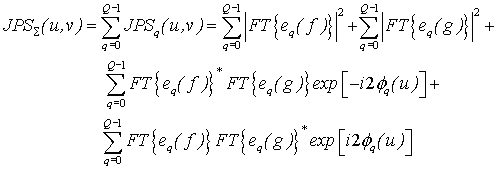


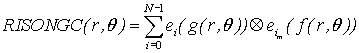
 is the circular harmonic component (CHC) of the
different binary slices of the reference object and
is the circular harmonic component (CHC) of the
different binary slices of the reference object and  are the polar coordinates.
are the polar coordinates.