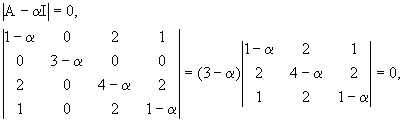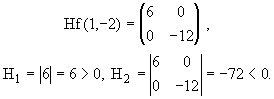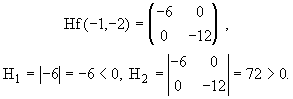MÉTODOS PARA LA DETERMINACIÓN
DEL SIGNO DE UNA FORMA CUADRÁTICA NO RESTRINGIDA:
AUTOVALORES DE UNA MATRIZ A
(matrices simétricas)
Se trata de obtener las raíces de la ecuación característica:
çA- a
Iç
= 0
donde A es la matriz cuadrada de orden n, I
es la matriz identidad de orden n.
|
|
DEFINIDAS
|
|
CONDICIÓN NECESARIA Y SUFICIENTE
|
|
DEFINIDA POSITIVA
|
ai >
0, " i=1,...,n
|
|
DEFINIDA NEGATIVA
|
ai <
0, " i=1,...,n
|
|
SEMIDEFINIDAS
|
|
CONDICIÓN NECESARIA Y SUFICIENTE
|
|
SEMIDEFINIDA POSITIVA
|
ai³
0, " i = 1,...,n
con al menos un aj = 0 y un ak>0,
1£ k,j£
n
|
|
SEMIDEFINIDA NEGATIVA
|
ai£
0, " i=1,...,n
con al menos un aj = 0 y un ak<0,
1£ k,j£
n
|
|
INDEFINIDAS
|
|
CONDICIÓN NECESARIA Y SUFICIENTE
|
|
INDEFINIDA
|
$ ai
> 0
$ aj
< 0
|
|
NULA
|
|
CONDICIÓN NECESARIA Y SUFICIENTE
|
|
NULA
|
ai =
0, " i = 1,...,n
|
MENORES PRINCIPALES CONDUCENTES DE A
(matrices simétricas)
Determinante de Orden 1: 1ªfila-1ªcolumna;
A1=ç
a11ç
Determinante de Orden 2: 2 primeras filas-2 primeras
columnas
A2= 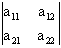
Determinante de Orden 3: 3 primeras filas-3 primeras
columnas
A3=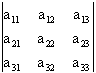
...
|
|
DEFINIDAS
|
|
CONDICIÓN NECESARIA Y SUFICIENTE
|
|
DEFINIDA POSITIVA
|
A1>0, A2>0, A3 > 0,... An>0
|
|
DEFINIDA NEGATIVA
|
A1< 0, A2 > 0, A3 < 0, A4
> 0,...
An > 0 si n es par
An < 0 si n es impar
|
|
SEMIDEFINIDAS
|
|
CONDICIÓN NECESARIA
|
|
çAç
= 0
|
|
CONDICIÓN SUFICIENTE
|
|
SEMIDEFINIDA POSITIVA
|
A1 > 0, A2 > 0, A3 > 0, ... Ar
> 0
Ar+1 = 0, ..., An = 0
con r = rango(A)
|
|
SEMIDEFINIDA NEGATIVA
|
A1 < 0, A2 > 0, A3 < 0,
A4 > 0,...
Ar > 0 si n es par
Ar < 0 si n es impar
Ar+1 = 0, ..., An = 0
con r = rango(A)
|
|
NULA
|
|
A= Q (matriz nula)
|
MENORES PRINCIPALES DE A
(matrices simétricas)
Determinantes construidos a partir de la diagonal principal:
DE ORDEN 1:
Cualquier determinante de orden uno construido a partir de la diagonal
principal de la matriz A. Resulta al tomar una fila cuyo orden (primero,
segundo, tercero, etc.) coincida con el de la columna elegida. Por ejemplo:
1ªfila-1ªcolumna; A1=ç
a11 ç (conducente)
2ªfila-2ªcolumna; ç a22ç
3ªfila-3ªcolumna; ç a33ç
4ªfila-4ªcolumna; ç a44ç
5ªfila-5ªcolumna; ç a55ç
6ªfila-6ªcolumna; ç a66ç
DE ORDEN 2:
Cualquier determinante de orden dos construido a partir de la diagonal
principal de la matriz A. Resulta al tomar dos filas cuyo orden (primero,
segundo, tercero, etc.) coincida con el de las dos columnas elegidas. Por
ejemplo:
1ª, 2ª filas-1ª, 2ª columnas (conducente): A2
=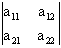
1ª,3ª filas- 1ª,3ª columnas: 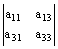
3ª,7ª filas- 3ª,7ª columnas: 
2ª,5ª filas- 2ª,5ª columnas: 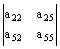
DE ORDEN 3:
Cualquier determinante de orden tres construido a partir de la diagonal
principal de la matriz A. Resulta al tomar tres filas cuyo orden (primero,
segundo, tercero, etc.) coincida con el de las tres columnas elegidas.
Por ejemplo:
3 primeras filas-3 primeras columnas (conducente): A3 =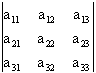 ; ;
1ª, 3ª, 4ª filas y columnas: 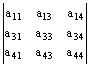 ; ;
2ª, 4ª, 5ª filas y columnas: 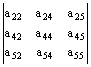 ; ;
|
|
DE ORDEN 4:
Cualquier determinante de orden cuatro construido
a partir de la diagonal principal de la matriz A. Resulta al tomar cuatro
filas cuyo orden (primero, segundo, tercero, etc.) coincida con el de las
cuatro columnas elegidas. Por ejemplo:
4 primeras filas-4 primeras columnas (conducente):
A4= ; ;
1ª,3ª, 5ª, 6ª filas y columnas: 
...
|
|
DEFINIDAS
|
|
CONDICIÓN NECESARIA Y SUFICIENTE
|
|
DEFINIDA POSITIVA
|
Todos los menores principales positivos.
|
|
DEFINIDA NEGATIVA
|
Todos los menores principales
-
positivos, los de orden par.
-
negativos, los de orden impar.
|
|
SEMIDEFINIDAS
|
|
CONDICIÓN NECASARIA Y SUFICIENTE
|
|
SEMIDEFINIDA POSITIVA
|
-
Determinante nulo, ç Aç
= 0
-
Todos los menores principales:
-
No negativos.
|
|
SEMIDEFINIDA NEGATIVA
|
-
Determinante nulo, ç Aç
= 0
-
Todos los menores principales:
-
No negativos, los de orden par.
-
No positivos, los de orden impar.
|
|
NULA
|
|
A= Q (matriz nula)
|
|
INDEFINIDAS
|
|
CONDICIONES SUFICIENTES
|
| 1.- Determinante no nulo y no se verifica la
CN y S de definida (ni DP ni DN) de menores principales conducentes.
2.- No se verifica ninguna de las CN y S anteriores de Definida ni de
Semidefinida: caso particular:
-
Menor principal de orden par negativo.
|
Ejercicios resueltos
0.- Estudie el signo de la forma cuadrática
representada por
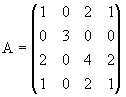 .
.
Solución:
Según el método de los menores principales conducentes:

El rango de A es 2, es decir, sólo hay dos columnas, o filas,
linealmente independientes, pues la tercera columna es el resultado de
multiplicar la primera por 2, y la cuarta columna es exactamente la primera.
Las dos primeras columnas son Linealmente Independientes (L.I.), como se
muestra con A2 > 0.
Se tiene, pues, que A1 > 0, A2 > 0, A3
= A4 = 0, con rg(A) = 2, por lo que se verifica la condición
suficiente de semidefinida positiva (menores principales conducentes positivos
hasta el de orden igual al rango de la matriz, y a partir del menor de
orden inmediato superior al del rango se anulan todos). Por tanto, la matriz
A es SEMIDEFINIDA POSITIVA.
Aplicando el método de los autovalores, se tiene:
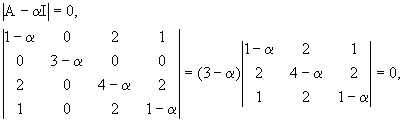
(3-a )[ (1-a
)(4-a )(1-a )+4+4-(4-a
)-4(1-a )-4(1-a )]
=
= (3-a )[ (1-a
)2(4-a )+8-4+a
-4+4a -4+4a] = (3-a
)[ (1-2a +a2)+9a
-4] =
= (3-a )[ 4-8a
+4a2-a
+2a2-a3+9a
-4] = (3-a )[
6a2--a3]=
0.
Una solución viene dada por:
3-a = 0 ®a1
= 3,
O bien por, 6a2-a3
= 0 ® a2
(6- a ) = 0, cuya solución viene dada
por a2=0®a2=a3=0;
o bien por 6 - a = 0 ®a4
= 6.
Los autovalores son a1 = 3, a2
= a3 = 0, a4
= 6. Todos son no negativos y existe al menos uno positivo y otro nulo.
Por tanto, A es SEMIDEFINIDA POSITIVA.
1.- Estudie el signo de la matriz

en los puntos (1,2), (1,-2), (-1,2) y (-1,-2). ¿Qué signo
tiene en R2?.
Solución:
En el (1, 2) se tiene
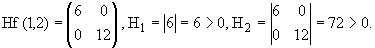
Todos los menores principales conducentes son positivos, por lo que
Hf(1,2) es DEFINIDA POSITIVA.
En el (1, -2) se tiene
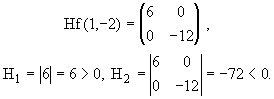
No se cumple la condición necesaria y suficiente de DEFINIDA
POSITIVA, pues todos los menores principales conducentes no son positivos.
No se cumple la condición necesaria y suficiente de DEFINIDA NEGATIVA,
pues todos los menores principales conducentes de orden par no son positivos,
H2<0, ni los de orden impar negativos, H1>0. No
cumple la condición necesaria de SEMIDEFINIDA POSITIVA o NEGATIVA,
H2 no es nulo, como no es NULA, Hf(1,-2) es INDEFINIDA. Se podía
haber concluido que es INDEFINIDA porque existe un menor principal de orden
par negativo, H2<0. Si se obtienen los autovalores, se tiene
a1=6
y a2=-12, uno positivo y otro negativo,
lo que permite llegar a la misma conclusión.
En el (-1, 2) se tiene

Como en el punto (-1, 2), no se cumple la condición necesaria
y suficiente de DEFINIDA POSITIVA, ni de DEFINIDA NEGATIVA. Tampoco cumple
la condición necesaria de SEMIDEFINIDA POSITIVA o NEGATIVA, H2
no es nulo. Como no es una matriz NULA, Hf(-1, 2) es INDEFINIDA. También
se podía haber concluido que es INDEFINIDA porque existe un menor
principal de orden par negativo, H2<0. Los autovalores son
a1=-6
y a2=12, uno negativo y otro positivo,
lo que permite llegar a la misma conclusión.
En el (-1, -2) se tiene
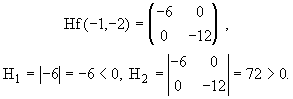
Todos los menores principales conducentes de orden par son positivos
y los de orden impar negativos, por lo que Hf(-1, -2) es DEFINIDA NEGATIVA.
Como existen puntos en R2 donde Hf es indefinida, o bien
para unos puntos es definida positiva y para otros es definida negativa,
se concluye que en R2 es "Indefinida".
NOTA: En R2++ es Definida positiva. En R2+
es "semidefinida positiva" (DP en unos puntos, SDP en otros, NULA en el
origen). En R2-- es definida negativa., mientras
que en R2- es "SDN" (DN en unos puntos, SDN en otros,
NULA en el origen)
Ejercicio propuesto:
Determine el signo de la forma cuadrática representada por la
siguiente matriz:

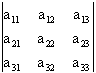
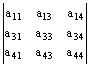 ;
;
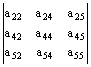 ;
; ;
;

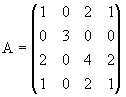 .
.