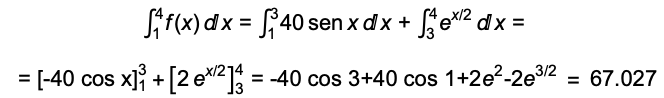Vídeos de Matemáticas I
En esta página tienes varios vídeos relacionados con la
asignatura Matemáticas I. Para verlos en móviles o tablets tal vez
tengas que pinchar en el icono 
que verás debajo de donde debería verse
el vídeo.
Matrices
- Repaso de
matrices (13 min)
Repaso de los conceptos básicos sobre matrices, incluyendo el
producto de matrices. Se corresponde con la sección 17.1 del
libro.
Puedes practicar el producto de matrices con el ejercicio 1 de
la página 275 y 280.
- Cálculo de
determinantes (7 min)
Repaso del cálculo de determinantes de matrices hasta de orden
3x3. Se corresponde con el principio de la sección 17.2 del
libro.
Puedes practicar el cálculo de determinantes 3x3 con el
ejercicio 2 de la página 281.
- Cálculo de
inversas (15 min)
Repaso del cálculo de matrices inversas. Se corresponde con la
sección 17.4 del libro.
Puedes practicar el cálculo de matrices inversas con el
ejercicio 2 de la página 276 y los ejercicios 4 y 5 de la página
281.
- Cálculo de
determinantes de orden 4x4 y superior (23 min).
Se explica cómo reducir el orden de un determinante hasta
reducirlo a uno 3x3. Se corresponde con el final de la sección
17.2 del libro, a partir del ejemplo 3b.
Puedes practicar el cálculo de determinantes 4x4 con los
ejercicios 2 y 3 de la página 276 y el ejercicio 3 de la página
281.
Cálculo de derivadas
- Descomposición
de expresiones algebraicas (18 min)
Aquí se explica lo necesario para entender la estructura de las
funciones que vamos a manejar, imprescindible, entre otras
cosas, para derivarlas correctamente. Se corresponde con el
final de la sección 1.3 del libro, a partir de la página 21.
Puedes practicar con el ejercicio 9 de la página 31, y también
analizando las funciones de los ejercicios 6 y 7 de las páginas
107-108.
- Cálculo de
derivadas I (34 min)
Aquí se explica el uso básico de las reglas de derivación. Se
corresponde con el principio del tema 6 del libro, hasta la
sección 6.3 incluida.
- Cálculo de
derivadas II (16 min)
Aquí se explica el uso práctico de la regla de la cadena para
derivar funciones compuestas. Se corresponde con la sección 6.4
del libro.
- Cálculo de
derivadas III (22 min)
Aquí se explican las reglas para derivar productos y cocientes.
Se corresponde con las secciones 6.5 y 6.6 del libro.
- La
diferencial de una función (9 min)
Ejemplo de cálculo y uso de la diferencial de una función para
aproximar un incremento. Se corresponde con el ejemplo 1 de la
sección 10.1 del libro.
- La
regla de la cadena (14 min)
Ejemplo de uso de la regla de la cadena para derivar funciones
compuestas. Se corresponde con el ejemplo 4 de la sección 11.1
del libro.
Cálculo de integrales
- Cálculo
de límites (23 min)
Algunos ejemplos de cálculo de límites.
- Cálculo de
primitivas (29 min)
Se explican las reglas básicas para calcular primitivas
inmediatas. Se corresponde con las secciones 12.1 y 12.2 del
libro (aunque en el vídeo están numeradas por error como 11.1 y
11.2).
- Ejemplos de
integrales inmediatas (34 min)
Ejemplos de aplicación de las reglas explicadas en el vídeo
anterior. Concretamente, se resuelven algunos apartados del
ejercicio 1 de la página 200 (desde el 4 hasta el 14). Puedes
practicar con el ejercicio 2 de la página 200 (hasta el apartado
26).
Errata: En el minuto 3:49 al
resolver la integral debe poner 2x5 en lugar de 25x4.
- Integración por
partes (22 min)
Se explica el método de integración por partes. Se corresponde
con la sección 12.3 del libro.
Errata: En el minuto 19:50 falta un
signo menos en la última integral escrita, con lo que el
resultado final correcto es:
- Cálculo
de una integral impropia (17 min)
Conceptos teóricos
- Continuidad
(46 min)
Este vídeo trata de explicar el concepto de continuidad y su
importancia sin exceder el nivel de la asignatura.
- Límites
(33 min)
Aquí se explica el concepto de límite, siempre dentro de lo que
permite el nivel de la asignatura.
- Derivadas (43
min)
Se explica la definición y la interpretación geométrica de las
derivadas parciales.
- Diferenciabilidad
(54 min)
En los primeros 37 minutos se explica el concepto de
diferenciabilidad. En los 17 minutos restantes se explican los
conceptos de dirección de máximo crecimiento, máximo
decrecimiento y crecimiento nulo.
- La integral de
Riemann (35 min)
Se explica la definición de integral de Riemann. Errata
En el minuto 29 falta un cuadrado en una
fórmula. La versión correcta es:
