It is well known that many structures found in Nature correspond to mathematical structures, geometrical ones in particular. One of such cases are animals having a shell with spiral structure, like nautilus.

Fibonacci's series is defined recursively as follows:

a₁ = 1

a₂ = 1

a_n = a_n-1 + a_n-2, for every n > 2.

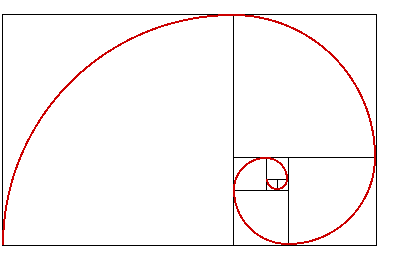
There are several ways to represent Fibonacci's series as an spiral. The most usual is by drawing several squares, their sides being the terms in the series. The spiral is built by drawing arcs of circles whose radii are the sides of the squares:

The shape of the shell of nautilus fits very exactly a Fibonacci's spiral based on equilateral triangles. We first draw several equilateral triangles, their sides being the terms in the series. Then we build the spiral by drawing arcs of the circles circumscribed to the triangles.

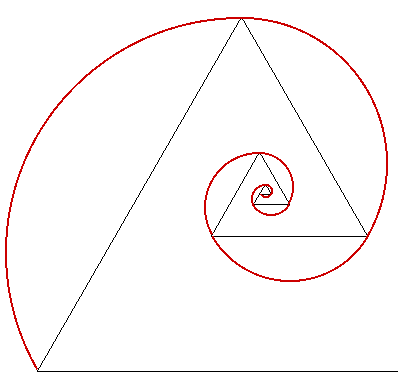
A visual difference between two Fibonacci's spirals is the opening of the curves. By comparing the two spirals in the figures above, we can see the difference between the shapes of Fibonacci's spirals generated by squares and equilateral triangles. In both cases I have used the same length unit to draw the first polygon.