References: Donat and Marquina, JCP, 125, 42 (1996)
Donat, Font, Ibáñez and Marquina, JCP, 146, 58 (1998)
- No ``artificial" averaged states at cell interfaces
- Marquina's numerical flux is as follows
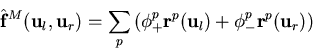 |
(110) |
where
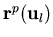 ,
,
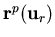 ,
are the right (normalized) eigenvectors of the Jacobian matrices
,
are the right (normalized) eigenvectors of the Jacobian matrices
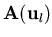 ,
,
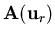
- The sided local characteristic variables and fluxes:
where
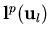 ,
,
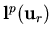 ,
are the (normalized) left eigenvectors
,
are the (normalized) left eigenvectors
- If eigenvalue
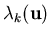 does not change
sign in
does not change
sign in
![$[{\bf u}_l,{\bf u}_r]$](img644.png) , then (upwind)
, then (upwind)
If
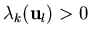 then
then
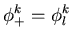
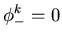
else
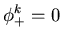
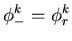
endif
else (entropy-satisfying local-Lax-Friedrichs)
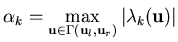
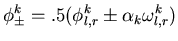
endif
where
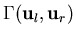 is a curve in phase space connecting
is a curve in phase space connecting
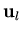 and
and 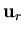
- For any hyperbolic system where the
fields are either genuinely nonlinear or linearly degenerate, we can
test the possible sign changes of
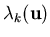 by checking the sign of
by checking the sign of
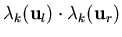
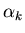 can also be determined as
can also be determined as
- Interesting properties:
- Designed for general hyperbolic systems of conservation laws
- When applied to constant-coefficient one-dimensional systems
yields the exact solution to the Riemann problem
- Able to handle ultrarelativistic flows with great accuracy
- The dissipation of the scheme eliminates undesired numerical ``pathologies":
- overheating in shock reflections
- long wavelength noise behind slowly moving shocks
- ``carbuncle" formation in hypersonic flow past blunt bodies
- Extended to relativistic hydrodynamics in
Donat, Font, Ibáñez and Marquina, JCP, 146, 58 (1998)
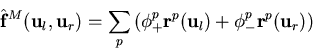
![]() ,
,
![]() ,
are the right (normalized) eigenvectors of the Jacobian matrices
,
are the right (normalized) eigenvectors of the Jacobian matrices
![]() ,
,
![]()
![]() ,
,
![]() ,
are the (normalized) left eigenvectors
,
are the (normalized) left eigenvectors
![]() is a curve in phase space connecting
is a curve in phase space connecting
![]() and
and ![]()