Next: 4.7 One-dimensional numerical tests Up: 4 Métodos en diferencias Previous: 4.5 Multidimensional problems
References: Banyuls, Font, Ibáñez, Martí and Miralles, ApJ, 476 221 (1997)
Font, Miller, Suen and Tobias, Phys. Rev. D (1999) in press
gr-qc/9811015
Conserved Variables:
rest-mass density (![]() ),
momentum density in the
),
momentum density in the ![]() -direction (
-direction (![]() ) and total energy
density (
) and total energy
density (![]() ). In terms of the primitive variables
). In terms of the primitive variables
![]()
where
![]() ,
,
![]() and
and
![]() (Lorentz factor)
(Lorentz factor)
![]() with
with
![]() .
.
Fundamental System (Hyperbolic):
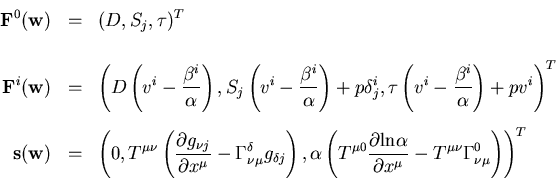
where
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Numerical Integration:
Eigenvalues:
Right-eigenvectors:
![\begin{displaymath}
{\bf r}_{\pm} =
\left[ \begin{array}{c}
1 \\
h W
\left( ...
...displaystyle{\frac{{\cal K}}{h W}}} \\
\end{array} \right]
\end{displaymath}](img746.png)
![\begin{displaymath}
{\bf r_{0,2}} =
\left[ \begin{array}{c}
W v_y \\
h \left...
..._z }}\right) \\
W v_z (2hW - 1) \\
\end{array} \right]
\end{displaymath}](img747.png)
with
![]() ,
,
![]() ,
,
![]() and
and
![]()
In numerical relativity the GRH equations must be solved in conjunction with the gravitational field equations (Einstein equations)
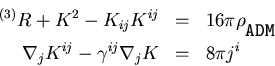
with