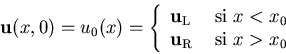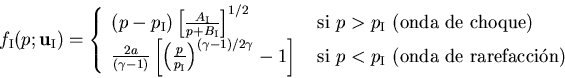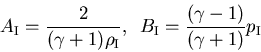- El Problema de Riemann es un problema de valores iniciales
discontinuos de la forma:
con
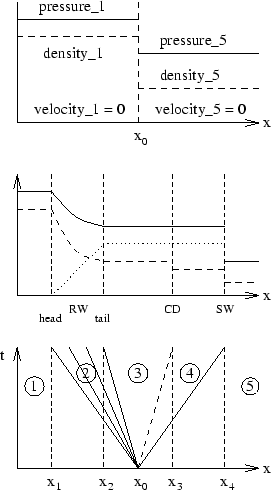
- El dato inicial no tiene escala espacial definida, por lo
que su solución es autosemejante:
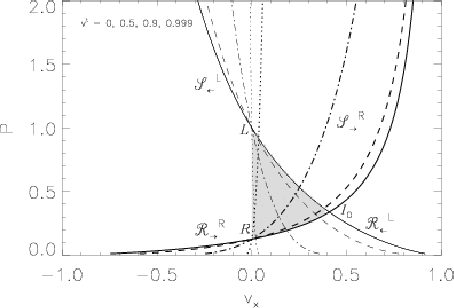
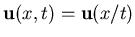 . La solución consiste en dos estados constantes
(
. La solución consiste en dos estados constantes
(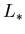 ,
, 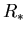 ) separados de los estados iniciales por ondas de
choque (
) separados de los estados iniciales por ondas de
choque (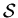 ) y/o rarefacciones (
) y/o rarefacciones (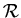 ) con una
discontinuidad de contacto (
) con una
discontinuidad de contacto (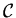 ) entre ellos:
) entre ellos:
(
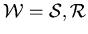 ;
las flechas (
;
las flechas (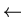 /
/ 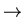 ) indican la dirección
desde la que los elementos de fluido atraviesan la correspondiente
onda).
) indican la dirección
desde la que los elementos de fluido atraviesan la correspondiente
onda).
- Ondas de choque: Soluciones discontinuas de las ecuaciones de
Euler con flujo de masa a través de la discontinuidad. Los estados
a izquierda y derecha de la onda de choque y su velocidad están
relacionados mediante las condiciones de Rankine-Hugoniot. Las
ondas de choque son compresivas (las partículas de fluido
aumentan su presión al atravesarlas).
- Discontinuidades de contacto: Soluciones discontinuas de las
ecuaciones de Euler. A diferencia de las ondas de choque, a
través de la discontinuidades de contacto no hay flujo de masa. La
presión y la velocidad del fluido son iguales a ambos lados
de la discontinuidad de contacto.
- Ondas de rarefacción: Soluciones continuas autosemejantes de
las ecuaciones de Euler que conectan estados constantes. Las
partículas de fluido reducen su presión al atravesarlas.
- La solución para la presión en los estados
intermedios,
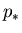 , de un problema de Riemann con una ecuación de
estado de gas ideal viene dada por la raíz de la ecuación
algebraica
, de un problema de Riemann con una ecuación de
estado de gas ideal viene dada por la raíz de la ecuación
algebraica
donde la función 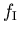 (
(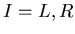 ) viene dada por:
) viene dada por:
donde 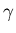 es el cociente de calores específicos del gas
ideal,
es el cociente de calores específicos del gas
ideal, 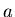 la velocidad del sonido y las constantes
la velocidad del sonido y las constantes 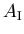 y
y
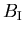 están
dadas por
están
dadas por
- La solución para la velocidad del fluido en el estado
intermedio,
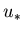 , viene dada por
, viene dada por
- Una vez obtenidas
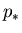 ,
, 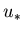 , se pueden obtener los valores
del resto de variables en los estados intermedios y las
velocidades de propagación de las ondas de choque, los extremos
de las rarefacciones y la discontinuidad de contacto, que
separan los diferentes estados constantes. Por último se pueden
obtener los valores de las variables en la rarefacción.
, se pueden obtener los valores
del resto de variables en los estados intermedios y las
velocidades de propagación de las ondas de choque, los extremos
de las rarefacciones y la discontinuidad de contacto, que
separan los diferentes estados constantes. Por último se pueden
obtener los valores de las variables en la rarefacción.
- Referencias:
- E.F. Toro, Riemann solvers and Numerical Methods for
Fluid Dynamics, Springer, 1997. Capítulo 4
- R. Courant, K.O. Friedrichs, Supersonic Flow and Shock
Waves, Springer, 1976. Epígrafes 80 y 81
- L.D. Landau, E.M. Lifshitz, Fluid Mechanics, Springer,
1987. Epígrafe 100
![\begin{displaymath}
\frac{\partial {\bf u}}{\partial t} + \frac{\partial {\bf F}...
...{c}
\rho u \\
\rho u^2 + p \\
u (E + p)
\end{array} \right]
\end{displaymath}](img787.png)