


Next: Sobre este documento...
Practica I (9 de abril de 2003)
El objetivo de esta práctica es la realización de un programa en C para calcular el intervalo de confianza de la media para un coeficiente de confianza dado, suponiendo que la muestra de que disponemos sigue una distribución normal con media y varianza desconocidas.
Sea
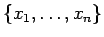 una muestra aleatoria de una variable aleatoria
una muestra aleatoria de una variable aleatoria
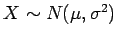 . Su media muestral viene dada por:
. Su media muestral viene dada por:
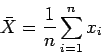 |
(1) |
y su cuasivarianza se define como:
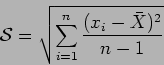 |
(2) |
Con esos ingredientes un intervalo de confianza con coeficiente de confianza 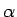 para la media
para la media 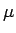 es:
es:
![\begin{displaymath}
I_\alpha=\left[\bar{X}-t_{n-1,\frac{1+\alpha}{2}}\frac{\math...
...+t_{n-1,\frac{1+\alpha}{2}}\frac{\mathcal{S}}{\sqrt{n}}\right]
\end{displaymath}](img7.png) |
(3) |
donde
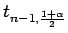 es el percentil de orden
es el percentil de orden
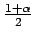 de la distribución
de la distribución 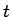 de Student con
de Student con 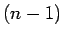 grados de libertad.
grados de libertad.
Utilizando el programa anterior vamos a resolver los problemas siguientes:
- Se han realizado 5 mediciones independientes y de igual precisión del peso atómico de la iodina y se encontraron los resultados {126.976, 126.974, 126.987, 126.976, 126.982}. Se pide calcular el verdadero valor de dicho peso atómico con una fiabilidad del 80 % y con una fiabilidad del 95 %.
- Calcula intervalos de confianza del 80 % y del 95 % para la media poblacional del número de
mg de hidroxipolina absorbidos por mg de masa intestinal en una población normal de
pacientes, a partir de la muestra {77.3, 61.2, 82.4, 75.9, 61.0, 70.2, 65.0, 80.0}.



Next: Sobre este documento...
2003-05-09
![]() una muestra aleatoria de una variable aleatoria
una muestra aleatoria de una variable aleatoria
![]() . Su media muestral viene dada por:
. Su media muestral viene dada por:
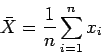
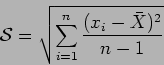
![]() para la media
para la media ![]() es:
es:
![\begin{displaymath}
I_\alpha=\left[\bar{X}-t_{n-1,\frac{1+\alpha}{2}}\frac{\math...
...+t_{n-1,\frac{1+\alpha}{2}}\frac{\mathcal{S}}{\sqrt{n}}\right]
\end{displaymath}](img7.png)