¡Hagamos mosaicos!

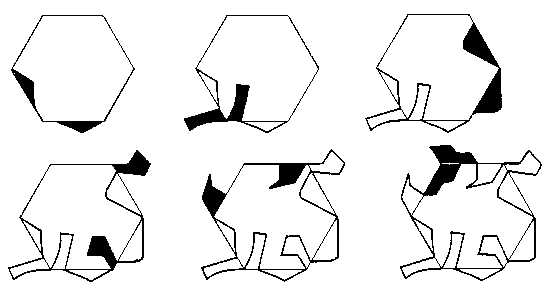
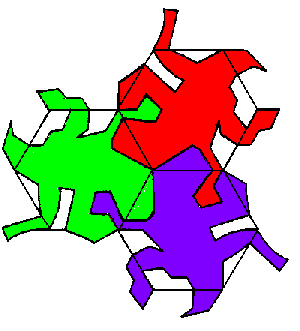
Una forma sencilla de conseguir mosaicos consiste en deformar los polígonos de un mosaico regular –formado por tríangulos equiláteros, cuadrados o hexágonos regulares– como en el ejemplo. El fundamento de la técnica es simple: eliminar una parte de un lado del polígono para añadirla en otro. Repetiremos este par de acciones siguiendo siempre el mismo criterio hasta que obtengamos la figura que deseemos que encajará con el resto en virtud del proceso de construcción que hemos seguido.

Podéis utilizar los siguientes mosaicos como fondo del escritorio de Windows:

Encontraréis más información en las páginas:

Stærðfræði í list Eschers.
— http://www.khi.is/~solrun/namsefni/escher/welcome.htm

Escher's Tessellations (en Totally tessellated). - In this section we will browse through some of the tessellation designs created by M. C. Escher. At the same time, we will discuss the techniques used in hopes of being able to create our own Escher-like tessellations.
— http://library.thinkquest.org/16661/escher/tessellations.1.html

Mosaicos o teselados. - "¡Cómo me gustaría aprender a dibujar mejor! Hacerlo bien requiere tanto esfuerzo y perseverancia... A veces los nervios me llevan al borde del delirio. Sólo es cuestión de batallar sin descanso con una autocrítica constante e implacable. Pienso que crear mis grabados sólo depende de querer realmente hacerlo bien. En su mayor parte algunas cosas como el talento son naderías. Cualquier escolar con unas pequeñas aptitudes podría dibujar mejor que yo. Lo que normalmente falta es el deseo incontenible de expresarse, apretando los dientes con obstinación y diciendo: - Aunque sé que no puedo, sigo queriendo hacerlo." Maurits C. Escher .
— http://www.geocities.com/teselados

Mosaicos. - Si colocamos polígonos iguales o distintos, uno al lado de otro, cubriendo el plano, de manera que no queden huecos, habremos construido un mosaico. Los mosaicos pueden ser más o menos variados, pero todos ellos tienen un motivo mínimo que se repite.
— http://www.edu.aytolacoruna.es/centros/iesadormideras/mosaicos/index.html

The 17 plane symmetry groups (en la página personal de David E. Joyce ). - The various planar patterns can by classified by the transformation groups that leave them invariant, their symmetry groups. A mathematical analysis of these groups shows that there are exactly 17 different plane symmetry groups. Note that clicking on a small image below will take you to a discussion of the associated symmetry group (as will selecting the name of the group in the headings below).
— http://140.232.1.5/~djoyce/wallpaper/seventeen.html

Volver a la página de inicio

Envía tus comentarios