Supernova Explosions:
Abstract:
We study the amplification of magnetic fields in the collapse and the post-bounce evolution of the core of a non-rotating star of 15 M⊙ in axisymmetry. To this end, we solve the coupled equations of magnetohydrodynamics and neutrino transport in the two-moment approximation. The pre-collapse magnetic field is strongly ampli- fied by compression in the infall. Initial fields of the order of 1010 G translate into proto-neutron star fields similar to the ones observed in pulsars, while stronger initial fields yield magnetar-like final field strengths. After core bounce, the field is advected through the hydrodynamically unstable neutrino-heating layer, where non-radial flows due to convection and the standing accretion shock instability amplify the field fur- ther. Consequently, the resulting amplification factor of order five is the result of the number of small-eddy turnovers taking place within the time scale of advection through the post-shock layer. Due to this limit, most of our models do not reach equipartition between kinetic and magnetic energy and, consequently, evolve similarly to the non-magnetic case, exploding after about 800 ms when a single or few high- entropy bubbles persist over several dynamical time scales. In the model with the strongest initial field we studied, 1012 G, for which equipartition between flow and field is achieved, the magnetic tension favours a much earlier development of such long-lived high-entropy bubbles and enforces a fairly ordered large-scale flow pattern. Consequently, this model, after exhibiting very regular shock oscillations, explodes much earlier than non-magnetic ones.
Movies:
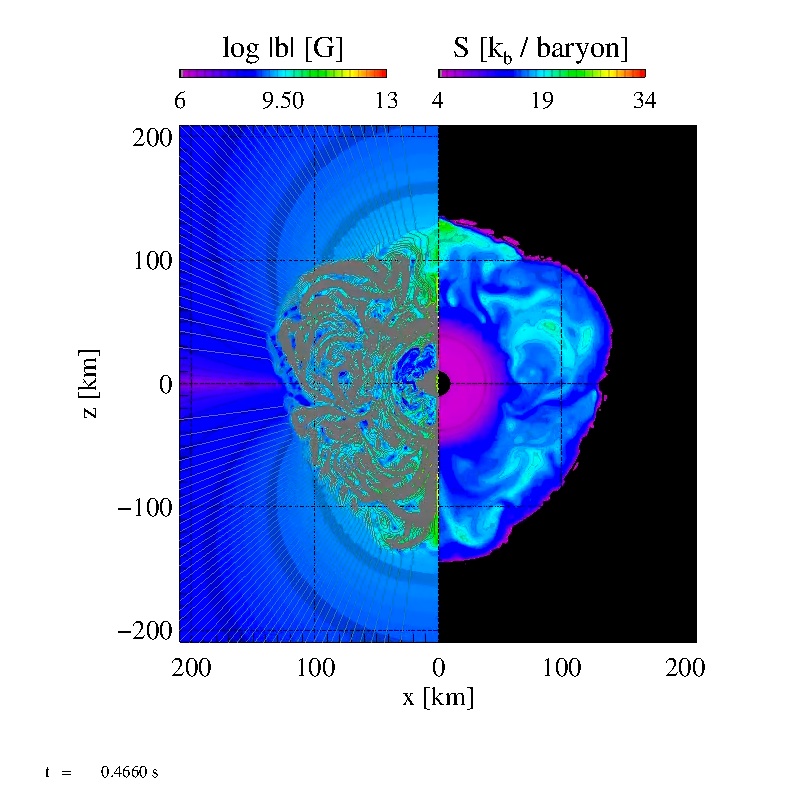 |
Evolution of Model B08 after bounce. We show the entropy per baryon on
the left and the logarithm of the magnetic field strength together with
magnetic field lines on the right. The movie sets in immediately before
core bounce and follows the dynamics of the post-shock region by
adjusting the length scale such that the shock remains near the outer
border of the displayed region. Soon after bounce, convection and the
SASI generate non-radial flows on intermediate scales and non-spherical
deformations of the stalled shock wave while neutrino heating increases
the mean entropy of the gas. It takes about 800 ms for a combination of
these effects to revive the shock wave. This latest stage is
characterised by the development of few large-scale bubbles of high
entropy. The magnetic field is amplified in the flow eddies and advected
onto the proto-neutron star (PNS). It has a negligible effect on the
dynamics. Click here to play the movie B08.avi |
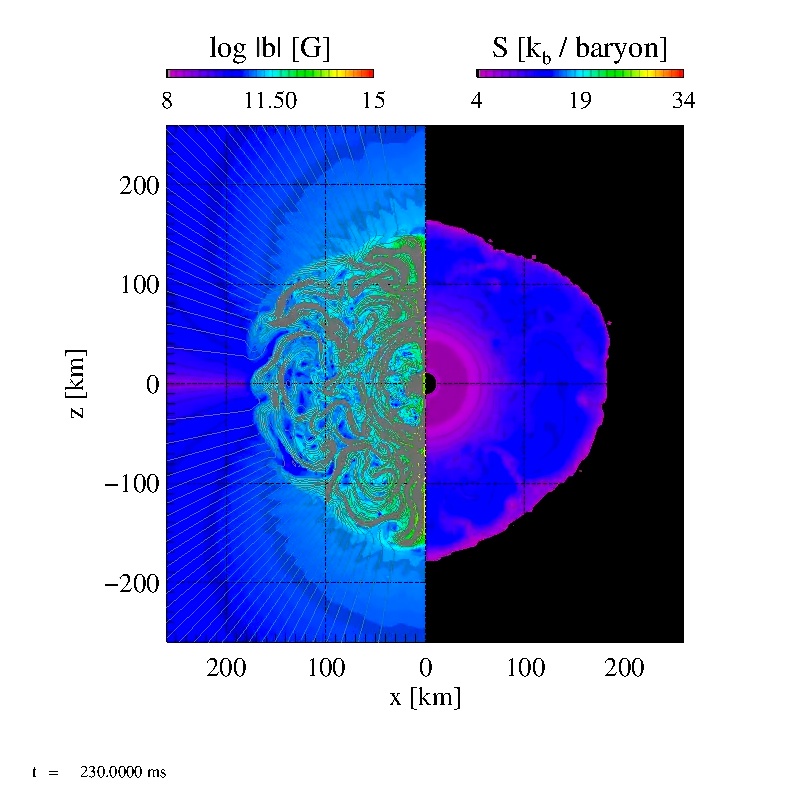 |
Same as B08.avi, but for Model B10. The magnetic field, though initially
100 times stronger, does not change the dynamics of the core.
Click here to play the movie B10.avi |
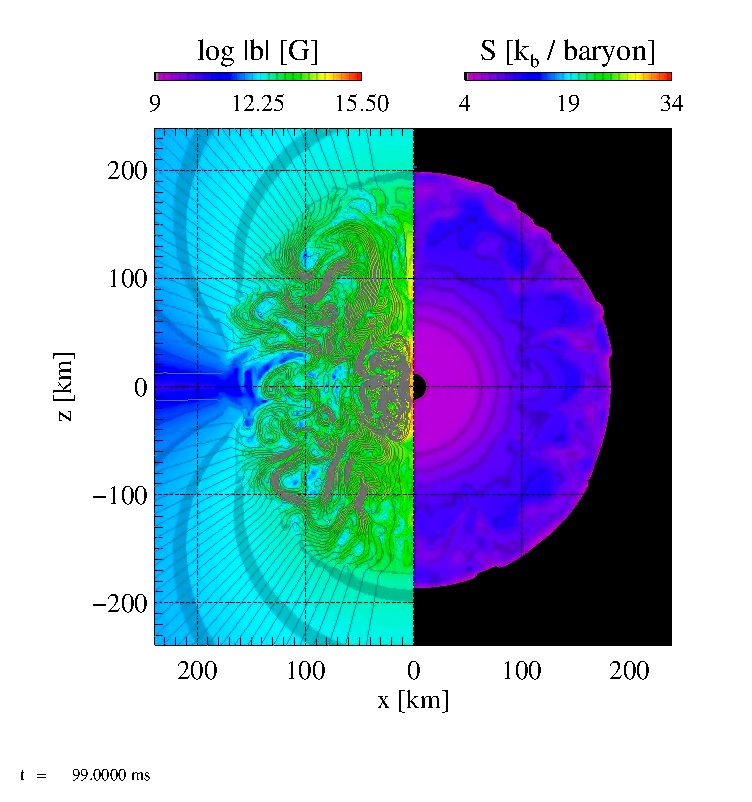 |
Same as B08.avi, but for Model B11. The effect of the magnetic field is
still weak.
Click here to play the movie B11.5.avi |
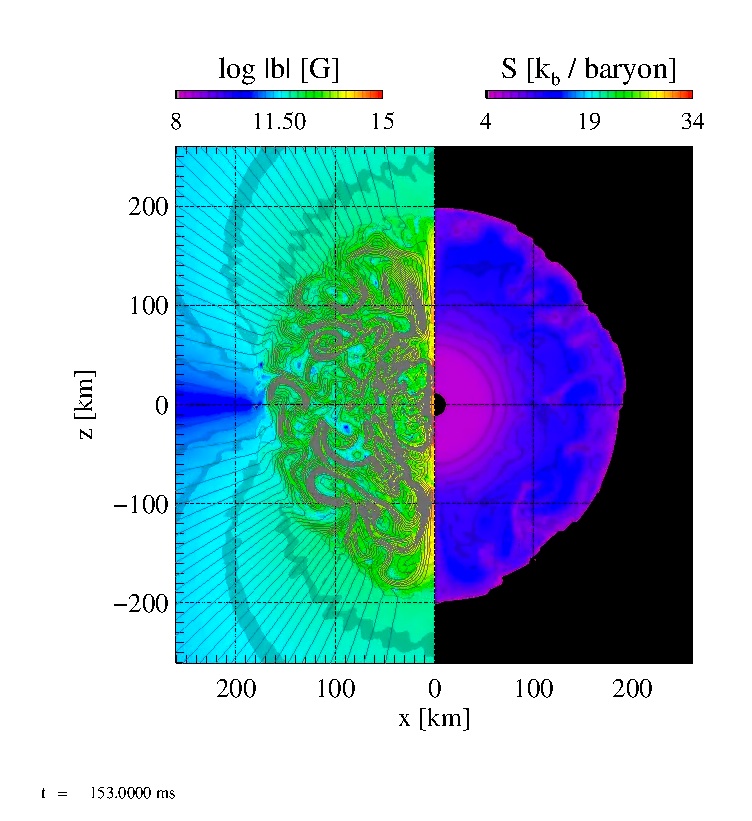 |
Same as B08.avi, but for Model B11.5. The magnetic field is
sufficiently strong to modify the post-shock flows. It suppresses the
dissipation of bubbles, leading to an earlier predominance of
large-scale bubbles and, consequently, an earlier onset of explosion.
Click here to play the movie B11.avi |
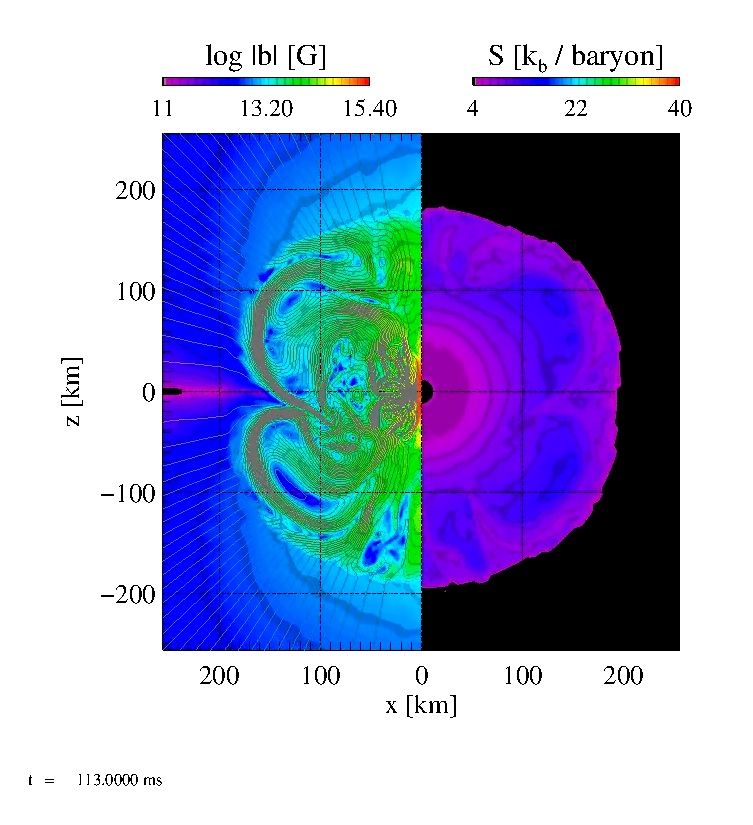 |
Same as B08.avi, but for Model B12. With the strongest field in our
sample, the post-shock region is always dominated by few very persistent
large-scale bubbles, and the shock wave exhibits very regular, slow
oscillations, which after only about 400 ms turn into a rapid expansion
of the shock wave.
Click here to play the movie B12.avi |
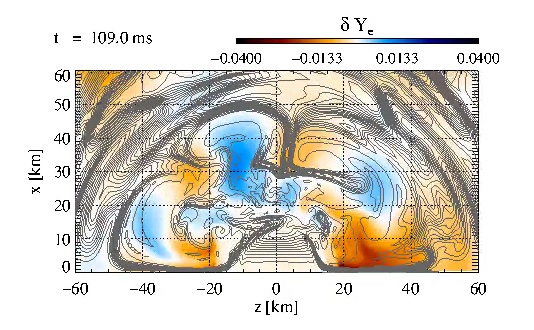 |
Evolution of the PNS of Model B10. We show the relative deviation of the
electron fraction of the gas from its angular average and magnetic field
lines. An extended layer of convective flows winds up the magnetic field
lines. At first, this process corresponds to an increase of the field
strength, but soon the decreasing width of the magnetic flux sheets
makes them susceptible to (numerical) dissipation, and the magnetic flux
is expelled to the upper, lower, and polar borders of the convection
zone. Meanwhile, magnetic flux is advected from higher radii and piles
up in lateral flux sheets in the stable layer surrounding the PNS. This
video corresponds to Fig. 7 from the paper.
Click here to play the movie Fig_07.avi |
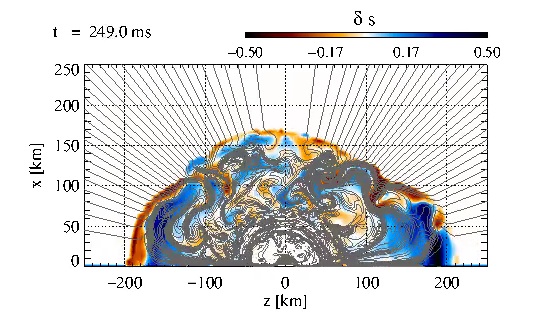 |
Convection, SASI and field amplification in Model B10. We show the
deviation of the relative entropy per baryon from the angular average
and magnetic field lines. The instability of the post-shock region is
dominated by eddies of intermediate size, until at late times a few
persistent larger bubbles develop. The magnetic field is amplified in
the eddies by a factor of about 5, but never gets strong enough to
affect the dynamics. This video corresponds to Fig. 12 from the paper.
Click here to play the movie Fig_12.avi |
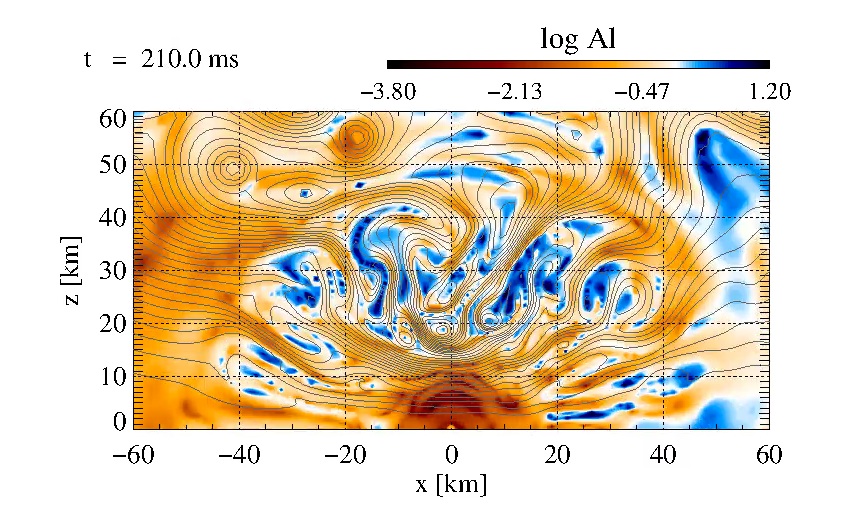 |
Evolution of the PNS of Model B12: field lines and the logarithm of the
Alfvén number of the flow. Regions where the magnetic field has larger
energy than the flow show up in red. Suppressed by the strong magnetic
field, convection is considerably weaker than for Model B10. The polar
regions exhibit a thick column of radial field, whereas the equatorial
regions close to the surface of the PNS possess strong lateral fields.
This video corresponds to Fig. 14 from the paper.
Click here to play the movie Fig_14.avi |
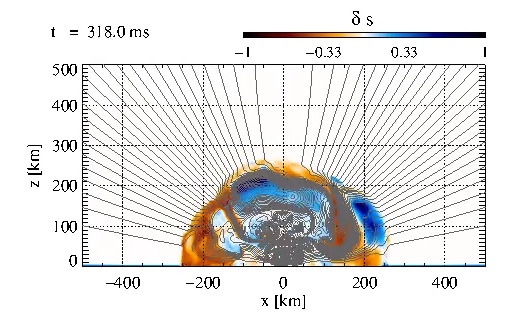 |
Same as Fig_12.avi, but for Model B12. The magnetic field is
sufficiently to impose a roughly quadrupolar structure on the flow. Two
large bubbles of increasing entropy persist for a long time and generate
very regular, slow shock oscillations eventually turning into a rapid
shock expansion. This video corresponds to Fig. 20 from the paper.
Click here to play the movie Fig_20.avi |
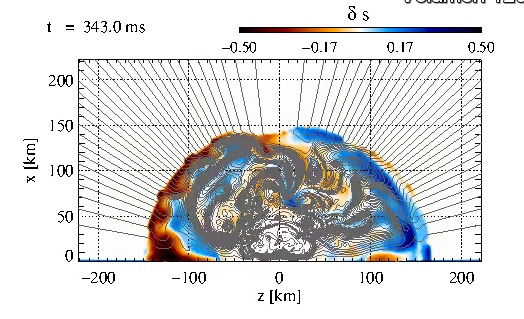 |
Same as Fig_12.avi, but for Model B11.5. This model represents an
intermediate case, where the magnetically aided generation of
large-scale bubbles and the transition to explosion occur later than in
Model B12. This video corresponds to Fig. 25 from the paper.
Click here to play the movie Fig_25.avi |
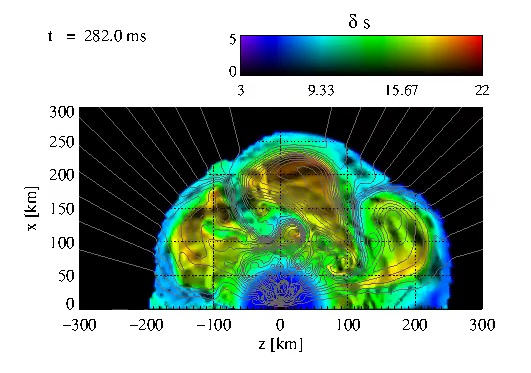
 |
Combined visualisation of magnetic field lines, entropy per baryon (hue)
and the normalised length scale of variations of the total pressure
(lightness of the colour scale) of Model B10. The latter quantity allows
for the identification of magnetosonic waves travelling in the
post-shock region. Complex flows develop in the unstable region and
amplify the field, very small-scale wave fronts travel back and forth
between the shock and the stable cooling layer on top of the PNS and
induce SASI oscillations, and neutrino heating gradually increases the
mean entropy. This video corresponds to Fig. 28 from the paper.
Fig_28.avi |
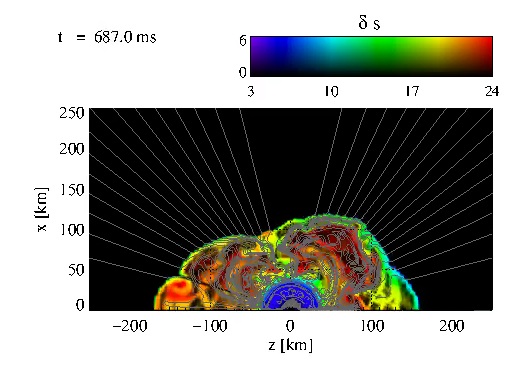
 |
Same as Fig_28.avi, but for Model B12. The presence of the strong field
leads to larger structures in the entropy as well as in the magnetosonic
waves. This video corresponds to Fig. 32 from the paper.
Click here to play the movie Fig_32.avi |
|