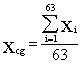
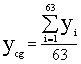
Donde n= 63
= número de municipios del área ;
Xi
e Yi son las coordenadas de cada uno de los puntos
|
|
|
|
CENTRO GRAVEDAD / CENTROS DE MASAS
La metodología de utilización de indicadores topométricos conocidos como "baricentros" , "centros de masas" o "centros de gravedad" no es habitual en en estudios económico- espaciales o socio-espaciales. Si bien algunos autores han utilizado esta metodología en alguna ocasión . Tenemos el primer antecedente en 1968 en el que la Revista Sindical de Estadística ( año XXIII , trimestre 1) publica un artículo de A. Sanz Sanchez , bajo el título "El baricentro de la población española " . Un segundo antecedente sería la obra de R. Tamames , " Los Centros de Gravedad de la Economía Española " publicada también en 1968 . Y un tercer , más reciente y último antecedente sería la obra de Angel y Pablo Alcaide "Centro de gravedad de la Economía Española" publicado en 1988 por FIES en su número 20.
El centro de gravedad de un cuerpo , concepto evidentemente sacado de la
física , es el punto donde aplicada una sola fuerza vertical
se podrían equilibrar todas la fuerzas de gravedad que actúan en dicho
cuerpo.
Si tomamos el A.M.V como un cuerpo , su centro de gravedad será
aquel punto capaz de equilibrarlo ante la presencia de una fuerza homogénea
en todo él. Por simplicidad tomamos el A.M.V como un cuerpo bidimensional ,
una simple superficie plana. Para simplificar todavía más tomamos la
superficie A.M de Valencia como una superficie discreta compuesta por 63
puntos singulares y perfectamante localizados en el espacio; dichos puntos
son los centros singulares de los 63 municipios que la componen .
El centro de gravedad de esta superficie simplificada ( discreta de 63 puntos ) sería el resultante de aplicar las simples expresiones para el cálculo de su abcisa y ordenada:
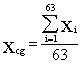
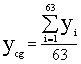
Donde n= 63
= número de municipios del área ;
Xi
e Yi son las coordenadas de cada uno de los puntos
Calculado dicho centro , este punto sería el "centro de gravedad" del Area Metropolitana de Valencia , evidentemente con un margen de error , pues se ha llevado a cabo de manera simplificada y discreta.
Estamos hablando del centro de gravedad o centro de masas de la variable espacio plano-superficie . De manera que estaríamos ante un presumible centro de masas obtenido al aplicar una carga unitaria a cada uno de sus puntos.


Si , como es normal , cada punto singular , cada municipio , tiene un valor distinto ( peso-carga-masa) en virtud de una determinada variable . Estaremos ante el centro de masas cuando sus coordenadas sean:
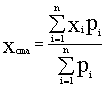
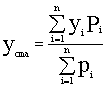
Donde n es el número de puntos
singulares ( en nuestro caso 63 municipios) Xi e Yi son
las coordenadas de cada uno de los puntos y Pi es el valor ( peso )
de la variable P para dicho punto i .
Las coordenadas Xcma e Ycma serían las
del centro de masas de la variable P aplicada al A.M. de Valencia tomada como
superficie plana .
Si bien los autores citados hablan de "centro de gravedad de
la población" o "centro de gravedad económico" , el término correcto sería
"centro de masas" pues es el resultante de aplicar " masas" o "pesos" a los
diversos puntos.
El centro de masas para una determinada variable supone el punto de equilibrio espacial para dicha variable. Es , por tanto , el punto donde hipóteticamente debiera aplicarse la "masa" de la variable para conseguir el mismo efecto que la aplicación detallada de la misma en cada uno de los puntos previos. Es por tanto un punto singular del A.M.V.
Comparando centros de masas de diversas variables con el centro de gravedad o bien centros de masas entre sí , podemos llegar a conclusiones inequívocas sobre el comportamiento espacial de dichas variables .
Ir a centros de masas calculados