DISTRIBUCIÓN BINOMIAL.
Nos encontramos con un modelo derivado de un proceso experimental puro, en el que se plantean las siguientes circunstancias.
·
Se realiza un número n de pruebas (separadas o separables).·
Cada prueba puede dar dos únicos resultados A y ÷
La probabilidad de obtener un resultado A es p y la de obtener un resultado à es q, con q= 1-p, en todas las pruebas. Esto implica que las pruebas se realizan exactamente en las mismas condiciones y son , por tanto ,independientes en sus resultados. Si se trata de extracciones, (muestreo), las extracciones deberán ser con devolución (reemplazamiento) , o bien población grande (M.A.S). A este respecto hagamos una consideración: si el proceso consiste en extraer individuos de una población y observar si poseen cierta característica: el parámetro n será el número de extracciones (tamaño muestral) y el parámetro p la proporción de individuos de la población que poseen la característica en cuestión. Se ha comentado que para que la probabilidad, de que en cada extracción obtengamos un individuo poseedor de la característica sea constante en todas la pruebas es necesario que las proporciones poblacionales no cambien tras cada extracción es decir se reemplace cada individuo extraído .Sin embargo si la población es muy grande, aunque no reemplacemos los individuos extraídos las variaciones en las proporciones de la población restante serán muy pequeñas y, aunque de hecho las probabilidades de, obtener un éxito varíen tras cada prueba, esta variación será muy pequeña y podremos considerar que son constantes .Ilustremos con un ejemplo:![]()
![]()
Supongamos que una ciudad hay 1000000 de habitantes de los
cuales 450000 son varones y 550000 son mujeres . Si extraemos un individuo al
azar la probabilidad. de que sea mujer será.
![]()
Si repetimos esta prueba varias veces y no reponemos "en el saco" al sujeto
extraído la probabilidad de obtener una mujer en cada siguiente extracción
variará, al variar la composición por sexos de la población restante. Sin
embargo, al ser la población tan grande, la variación de esta probabilidad con
cada sucesiva prueba será prácticamente despreciable y podremos considerar, en
la práctica que las probabilidades son constantes: en efecto:
Si, en la primera prueba obtenemos una mujer y no la
reintegramos a la población la de probabilidad de obtener una mujer en la
segunda prueba será:
![]()
Si por el contrario en la primera prueba se obtiene un varón la probabilidad de
obtener una mujer el siguiente será:
![]()
![]()
Por lo tanto bien podríamos considerar que la probabilidad de extraer una mujer
en sucesivas elecciones aleatorias es constante. En consecuencia, si
consideráramos el muestreo de 10 individuos de esa ciudad, aunque no
reemplazáramos las extracciones, la variable aleatoria x = número de mujeres
obtenidas en las diez extracciones, seguiría una distribución binomial de
parámetros n = 10 Y p= 0.55.
Sin embargo, si la población es pequeña, las variaciones de la probabilidad de éxito con cada prueba serán importantes sino se devuelve a la población original cada sujeto extraído .En este caso, no podremos considerar que p y q son constantes a lo largo de todo el proceso y el número de éxitos obtenidos en n pruebas será una variable aleatoria que no seguirá una distribución binomial sino una nueva distribución que estudiaremos , más tarde llamada hipergeométrica.
·
En estas circunstancias se aleatoriza de forma que variable aleatoria signifique:X = nº de resultados A que se obtienen en las n pruebas
Se plantean dos valores con variación por lo que tendremos
dos parámetros p y n , por lo que la distribución binomial se explicitará :
![]()
El campo de variación de la variable será {0,1,2,3,..., n}, por lo que no es
necesario comentar que es de carácter discreto. Así tendremos que si queremos
calcular la probabilidad de que X=1 en n pruebas , tendríamos 1 resultado A y
n-1 resultados no A.
|
Prueba 1 |
Prueba 2 |
Prueba 3 |
……. |
Prueba n |
Prueba |
|
|
No A |
No A |
No A |
No A |
No A |
A |
Resultado |
|
q |
q |
q |
q |
q |
p |
Probabilidad |
Por lo que la probabilidad de conseguir un resultado A sería
en principio , y dado que las pruebas son independientes
![]() . Lo que sería
correcto si el resultado A , lo fuera en la última prueba. Dado que nos es
indiferente en que prueba sea tendríamos que multiplicar esta probabilidad por
. Lo que sería
correcto si el resultado A , lo fuera en la última prueba. Dado que nos es
indiferente en que prueba sea tendríamos que multiplicar esta probabilidad por
![]() . Por lo que
tendríamos que:
. Por lo que
tendríamos que:
 generalizando
para cualquier valor de X , quedaría que la función de cuantía de la binomial
tiene como expresión
generalizando
para cualquier valor de X , quedaría que la función de cuantía de la binomial
tiene como expresión
![]()
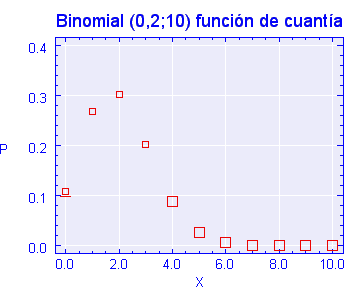
Gráficamente la función de cuantía quedaría de la siguiente manera , siempre dependiendo de los valores que tomen los parámetros . En este caso se trata de una B(0,2;10),siendo la representación gráfica de su función de cuantía:
La función de distribución será para cada valor k de la variable
![]()
Los indicadores-momentos (media y varianza) pueden obtenerse a partir de la función de cuantía (operador esperanza) o partiendo de F.G.M.:
Siendo la F.G.M.:
![]()
![]()
desarrollando el Binomio de Newton obtendríamos ,
![]()
También podríamos haber obtenido la F.G.M. , partiendo del
hecho de que la distribución o modelo binomial es la reiteración n veces del
modelo dicotómico, Así si:
![]() es decir
realizamos una prueba con probabilidad de éxito p , siendo la aleatoriación el
número de resultados A en esa prueba . Tendremos que un serie de pruebas
independientes (n) con probabilidad de A en cada prueba , será la agregación de
n dicotómicas . Si X es el número de resultados A en esas n pruebas y por tanto
una Binomial n,p. Así
es decir
realizamos una prueba con probabilidad de éxito p , siendo la aleatoriación el
número de resultados A en esa prueba . Tendremos que un serie de pruebas
independientes (n) con probabilidad de A en cada prueba , será la agregación de
n dicotómicas . Si X es el número de resultados A en esas n pruebas y por tanto
una Binomial n,p. Así
![]()
De esta manera si conocemos que la F.G.M de la dicotómica (Y) es
![]()
dado que
![]()
la F.G.M. de X (binomial) será el producto , n veces , de la
F.G.M de Y ( dicotómica) dado que las Y son independientes. Así
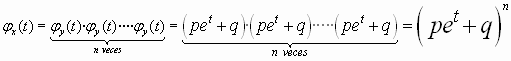
Mediante la aplicación del teorema de los momentos podemos calcular las ratios del modelo.
La media sería ![]()
![]() si hacemos t =0
si hacemos t =0
![]()
por lo que la media sería
![]()
![]()
Podríamos haber calculado la media partiendo de la binomial como reiteración de dicotómicas ; así
Si ![]() conociendo
que la media de Y= p
conociendo
que la media de Y= p
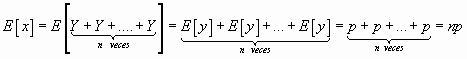
que lógicamente nos resulta con el mismo resultado
La varianza de la Binomial vendría dada por
![]()
Siendo
![]()
![]()
Así
![]()
Luego la varianza sería
![]()
Calculando la varianza de la binomial como reiteración de dicotómicas sería
Si
![]() conociendo que
la varianza de Y= pq
conociendo que
la varianza de Y= pq
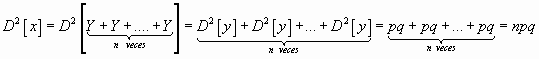
Partiendo de la F.G.M obtendríamos los diversos momentos ordinarios necesarios para el cálculo de otros coeficientes como el de asimetría y curtósis. Cuyas expresiones son las siguientes.
Coeficiente de Asimetría
![]() en el que se
puede comprobar que si p=q=0,5 su valor es cero, lo que nos indica simetría para
este valor del parámetro p , siendo el que fuere n
en el que se
puede comprobar que si p=q=0,5 su valor es cero, lo que nos indica simetría para
este valor del parámetro p , siendo el que fuere n
Coeficiente de Curtósis
![]() siendo mínimo
para p=q=0,5
siendo mínimo
para p=q=0,5
En cuanto a la Moda ,dado que es el valor de la variable con mayor probabilidad (maximiza su función de probabilidad). Tendremos que si Xo es el valor modal
P(Xo) ³ P(Xi) para cualquier valor de i , en particular se verificará que
P(Xo) ³ P(Xo +1) y P(Xo) ³ P(Xo-1) es decir que el valor de la función de cuantía para el valor modal será mayor que dicho valor para los valores anterior y posterior a la moda.
Sustituyendo por las correspondientes funciones de cuantía en ambas inecuaciones , llegaremos a la expresión :
pn - q £ Xo £ pn + p
Siendo Xo el valor modal
Generalmente será un único valor ( la parte entera de la
media), y podrán ser dos valores modales cuando pn + p ( ó pn-q) sea un número
entero. Como ejemplo: si lanzamos un dado 10 veces y queremos saber cúal es el
número más probable de ases que conseguiremos tendremos que calcula la moda en
un modelo B(1/6;10) .Aplicando la desigualdad anterior tendríamos : 1/6·10-5/6≤Mo≤1/6·10+1/6
. Es decir 5/6≤Mo≤11/6
Sólo existe un número natural que verifique esa cota , el 1 . Para que hubiera
más de una moda , ambos valores de la desigualdad debieran ser números naturales
como los valores de la variable X con distribución binomial
Teorema de adición en la binomial
Se dice que una distribución verifica el Teorema de adición, para alguno de sus parámetros, o que es reproductiva, si dadas 2 o más variables aleatorias independientes que siguen todas ellas una distribución de ese tipo con parámetros distintos, la variable suma de todas ellas sigue, también una distribución de ese tipo con parámetros la suma de los parámetros de las variables originales.
Este teorema se prueba siempre a partir de la F.G.M. Se procede obteniendo la F.G.M. de la distribución de la variable suma , que por ser las variables originales independientes será el producto de las F.G.M. de las distribuciones de las variables originales. Una vez obtenida la F.G.M. comprobaremos si efectivamente se trata de F.G.M. de una distribución de ese tipo con parámetros la suma de los parámetros de las distribuciones de las variables originales .En virtud del carácter recursivo de la operación suma , para demostrar el teorema basta con demostrar que se cumple para la suma de dos variables aleatorias.
Pues bien, la distribución binomial verifica el teorema de adición para el parámetro n , aunque no lo verifica para el. parámetro p (además es necesario para que se verifique el teorema que el parámetro p de las distribuciones de las variables originales sea el mismo) :
"La variable suma de dos o más variables binomiales independientes de parámetros (n1,p) : (n2,p) : ………….... se distribuye como una distribución binomial de parámetros ( n1+n2+…, p) "
En efecto :
sean X e Y dos variables alaeatorias independientes tales que:
![]()
![]()
pretendemos probar que
![]()
Conocemos que la F.G.M del modelo binomial es para X
![]()
siendo para Y
![]()
Dado que X e Y son independientes la F.G.M. de la distribución de la variables suma será el producto de las dos F.G.M.
![]()
que es la F.G.M. de una B( n1+n2, p).
Observesé que este teorema se utilizó para el cálculo de la F.G.M. de la Binomial como reiteración (suma) de Dicotómicas , con la salvedad de tomar a la Dicotómica como una Binomial de n = 1 , es decir adición de n binomiales B(1,p)