y la
probabilidad de éxito sea muy pequeña
.CONVERGENCIA BINOMIAL-POISSON.
Se puede probar que la distribución binomial tiende a converger a la distribución de Poisson cuando el parámetro n tiende a infinito y el parámetro p tiende a ser cero, de manera que el producto de n por p sea una cantidad constante. De ocurrir esto la distribución binomial tiende a un modelo de Poisson de parámetro l igual a n por p
Este resultado es importante a la hora del cálculo de
probabilidades , o , incluso a la hora de inferir características de la
distribución binomial cuando el número de pruebas sea muy grande
y la
probabilidad de éxito sea muy pequeña
.
El resultado se prueba , comprobando como la función de cuantía de una
distribución binomial con
y
tiende a una
función de cuantía de una distribución de Poisson con
siempre que este producto sea una cantidad constante ( un valor finito)
En efecto : la función de cuantía de la binomial es
Y llamamos
tendremos que:
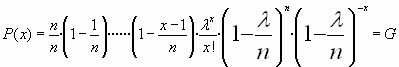
realizando 
que es la función de cuantía de una distribución de Poisson