
DISTRIBUCIÓN CAUSAL
La distribución causal no es, propiamente una distribución de probabilidad .La razón es que es aplicable en aquellos casos en que la probabilidad de un único y cierto valor de la variable es 1 y, para todo el resto de valores reales la probabilidad es cero. En consecuencia esta distribución sólo puede dar cuenta de fenómenos en los que la ocurrencia de un cierto suceso es segura y la ocurrencia de cualquier otro es imposible. En estos casos, obviamente, no existe azar, pero a través de esta distribución, nos resulta fácil ver la causalidad o el determinismo como un caso particular de azar o aleatoriedad.
Proceso experimental del que se puede hacer derivar.
Esta distribución puede hacerse derivar de un proceso puro o de Bernouilli si consideramos las siguientes
·
Se realiza un número definido de pruebas, N.
·
Cada una de las pruebas puede dar dos resultados mutuamente excluyentes :
A y no A
·
La probabilidad en cada prueba de obtener un resultado A es siempre la misma
(constante) y es igual a 1 , lógicamente la probabilidad de obtener en
cualquier prueba un resultado no A será cero.
·
(Derivación de la distribución) si en estas circunstancias aleatorizamos de
forma que la variable aleatoria X se defina como " el número de resultados
A obtenidos en N pruebas" la variable aleatoria X tendrá una
distribución causal (de parámetro N)
Características analíticas ,de la distribución
Es fácil comprobar que la
función de cuantía de esta distribución será
: 
Siendo la función de
distribución 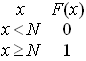
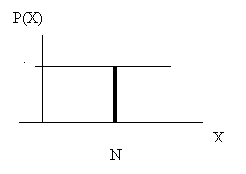
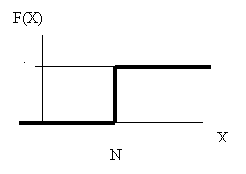
función de cuantía función de distribución
La media del modelo causal
será ![]()
Siendo la varianza ![]()
![]()