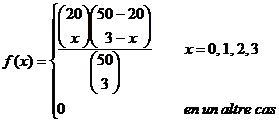
|
|
|
|
D’un grup de 50 individus, en triem tres a l’atzar (sense reemplaçament). Sabent que en el grup hi ha 30 dones, ¿quina és la probabilitat que els tres triats siguen homes?
En les condicions establertes –extracció sense reemplaçament d’una població dicotòmica–, la variable X = Nombre de mascles es distribueix com una hipergeomètrica de paràmetres M = = 20, N = 50 i n =3:
X ~ H(x; 20, 50, 3)
La funció de probabilitat d’aquesta distribució ve donada per:
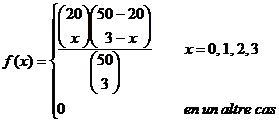
La probabilitat que els tres individus siguen homes és:
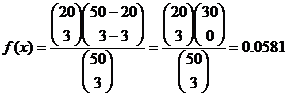
La distribució hipergeomètrica es deixa aproximar raonablement bé per la binomial a partir de certs valors dels paràmetres. És fàcil veure que, si la població és molt gran amb relació a la mostra, l’efecte de no reemplaçar a la població l’element que se n’ha extret és irrellevant i, per tant, podríem tractar la situació com una binomial sense risc de cometre un error important. També en casos menys evidents es poden abordar bones aproximacions a la distribució hipergeomètrica emprant una binomial. Com a regla empírica general es recomana assegurar-se que la relació de la grandària de la mostra respecte a la de la població és del 5% o inferior, és a dir, n/N < 0.05.
El paràmetres
de la binomial seran el mateix valor de n i un valor de
q,
equivalent a la proporció de “boles roges” en la població; és a dir:
![]() .
.

