REF.

 El nombre de telèfons mòbils que interrompen durant una hora de classe segueix una distribució de Poisson de paràmetre l = 1. Calcular la probabilitat que, al llarg d’una hora, sone un telèfon, com a mínim.

La probabilitat demanada és . Per calcular aquesta probabilitat, ens convé plantejar el problema en termes de l’esdeveniment complementari:

Com que X ~ P(x; 1), la funció de probabilitat és:

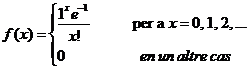
i la probabilitat demanada:

Una de les raons que justifiquen la “popularitat” de la distribució de Poisson és que permet aproximar probabilitats binomials substituint el parell de paràmetres  per l’únic paràmetre l, corresponent a la mitjana de la distribució. Aquesta aproximació serà més ajustada com[1] menor siga q i major n. Com a norma empírica s’assumeix que, a partir de n > 10 i q < 0.5, les aproximacions són acceptables.

Una altra característica important de la distribució de Poisson és la seua propietat reproductiva. Aquesta propietat –que comparteix, entre d’altres, amb la distribució normal– implica que la suma de variables de Poisson segueix també una distribució de Poisson.

?