DISTRIBUCIÓN DE PÓLYA
Se trata de un modelo discreto de gran utilidad en la ciencia actuarial dado que también es conocida como distribución del contagio. Su utilidad radica precisamente en que es capaz de medir la aleatoriedad del "contagio" no sólo de enfermedades ,como cabría suponer, sino de la extensión–propagación de la información sobre cualidades de los productos o servicios.
Se basa en un proceso , en cierto sentido , parecido al que sirve para dar lugar a la distribución hipergeométrica.
Sus características son las siguientes:
La distribución de Pólya puede derivarse de un proceso experimental puro o de Bernouilli con las siguientes características:
· El proceso consta de n pruebas , separadas o separables de entre un conjunto de N pruebas posibles.
· Cada una de las pruebas puede dar únicamente dos resultados mutuamente excluyentes: A y no A.
· En la primera prueba las probabilidades son :P(A)= p y P(A)= q ;con p+q=l.
Las probabilidades de obtener un resultado A y de obtener un resultado no A varían en las sucesivas pruebas, dependiendo de los resultados anteriores. De manera que aumentan las probabilidades del suceso que haya ocurrido en la prueba anterior , dado que si el resultado es A se aumenta la probabilidad de A para la siguiente prueba en un factor que denominamos de contagio (c) . En el caso de que el resultado fuera no A se procedería de la misma manera (aumentando las probabilidades de no A)
· (Derivación de la distribución) . Si estas circunstancias aleatorizamos de forma que la variable aleatoria X sea el número de resultados A obtenidos en n pruebas la distribución de X será una Pólya de parámetros N,n,p,c:
![]()
Planteemos un proceso como ejemplo:
En una urna existen N elementos N1 de carácter A y N2 de carácter no A
Evidentemente N= N1+N2
El experimento (prueba) consiste en la visualización del carácter de un elemento extraído
En la primera ocasión la
![]()
Si el resultado es A se introducen en la urna C elementos de carácter A
Si el resultado es no A se introducen en la urna C elementos de carácter no A
Las probabilidades habrán variado .Así
La probabilidad de obtener x resultados A en x pruebas sería:
![]()
dado que se realizan n pruebas , debemos considerar también
las n-x restantes y cuyo resultado sería "no A" .
Así
![]()
evidentemente realizaremos todas las n pruebas, luego tendríamos:
![]()
Dado que no tendrían porqué darse los resultados en ese determinado orden. La función de cuantía quedaría:
![]()
La esperanza matemática de esta distribución quedará como:
![]()
Siendo la varianza
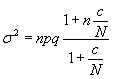
al cociente c/N se le conoce como fracción
inicial de contagio .
Proporción de individuos que se reponen o alcanzan el valor del resultado
de la prueba anterior.
Puede comprobarse que si C ( número de individuos que se introducen en la
urna con la característica del resultado anterior) es (-1).Estaríamos "no
reponiendo" la extracción , estaríamos , por tanto, ante una distribución
hipergeométrica .
Lo que podemos comprobar con su varianza.
Así : la varianza de la
hipergeométrica es
![]()
mientras que varianza de la Pólya hemos visto que era
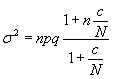 si
hacemos c = -1 tendremos
si
hacemos c = -1 tendremos
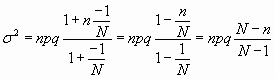 que es
la varianza de la hipergeométrica
que es
la varianza de la hipergeométrica