DISTRIBUCIÓN UNIFORME (DE V.CONTINUA)
La distribución o modelo uniforme puede considerarse como
proveniente de un proceso de extracción aleatoria .El planteamiento radica en el
hecho de que la probabilidad se distribuye uniformemente a lo largo de un
intervalo . Así : dada una variable aleatoria continua, x , definida en el
intervalo [a,b] de la recta real, diremos que x tiene una distribución uniforme
en el intervalo [a,b] cuando su función de densidad para
![]() sea:
sea:
![]() para x Î [a,b].
para x Î [a,b].
Su representación gráfica será :
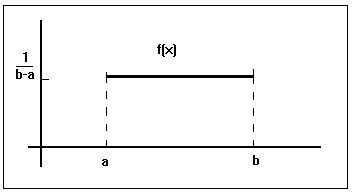
De manera que la función de distribución resultará:

Su representación gráfica será :
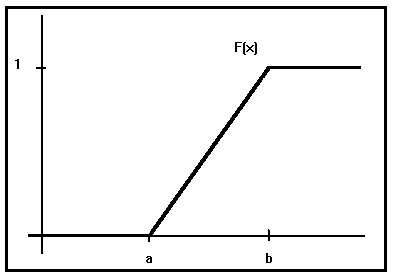
Este modelo tiene la característica siguiente : Si calculamos
la probabilidad del suceso
![]()
Tendremos:
![]()
Este resultado nos lleva a la conclusión de que la probabilidad de cualquier suceso depende únicamente de la amplitud del intervalo (D X) , y no de su posición en la recta real [a , b] . Lo que viene ha demostrar el reparto uniforme de la probabilidad a lo largo de todo el campo de actuación de la variable , lo que , por otra parte, caracteriza al modelo.
En cuanto a las ratios de la distribución tendremos que la media tiene la expresión:
![]()
La varianza tendrá la siguiente expresión:
![]()
de donde ![]()
![]()
por lo que
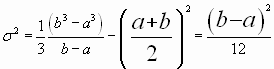
La función generatriz de momentos vendrá dada por :
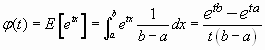
Lógicamente partiendo de esta función podríamos recalcular media y varianza gracias al teorema de los momentos