DISTRIBUCIÓN UNIFORME (DE V.DISCRETA)
Es una distribución muy sencilla que asigna probabilidades iguales a un conjunto finito de puntos del espacio.
Modeliza fenómenos en los que tenemos un conjunto de n sucesos posibles, cada uno de los cuales con la misma probabilidad de ocurrir. Si aleatorizamos de forma que cada uno de éstos sucesos se corresponda con un número natural del 1 al n obtendremos una distribución uniforme. Tendremos un único parámetro ; n
Diremos , por tanto que
![]()
Puede hacerse derivar en consecuencia de un proceso experimental de selección aleatoria, en el que la característica que consideramos en la selección sólo puede tomar un conjunto de n valores discretos y donde cualquiera de estos valores puede obtenerse con igual probabilidad.
Por su elementaridad no es una distribución de excesivo interés práctico.
Su función de cuantía definida para los valores de x ={ 1, 2,
, n} vendrá dada por la constante:
P(x) = l /n para x ={ 1, 2, , n}
Su función de distribución vendrá dada por
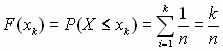
Puede comprobarse que su media será
![]()
![]()
su varianza será :
![]()
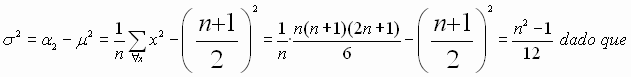
![]()
por último, su Función Generatriz de Momentos, quedará
expresada como
