INDEPENDENCIA ESTOCÁSTICA DE SUCESOS:
Dos sucesos A y B son estocásticamente independientes cuando la información sobre la ocurrencia de uno de ellos no modifica la probabilidad de que ocurra el otro.Esto es:
P(A/B) = P(A) o equivalentemente P(B/A) = P(B) ejemplo
CARACTERIZACIÓN DE LA INDEPENDENCIA: TEOREMA DE CARACTERIZACIÓN
A y B son independientes Û P(AÇB) = P(A).P(B) ya que si por
definición de independencia ![]()
y por definición de probabilidad condicionada ![]()
deberá cumplirse que ![]() .
.
Así , dos sucesos A y B son independientes si y sólo si ![]()
GENERALIZACIÓN DEL CONCEPTO DE INDEPENDENCIA (caracterización) PARA n SUCESOS
Un número finito o infinito de sucesos ![]() son mutuamente
independientes si dados los subíndices
son mutuamente
independientes si dados los subíndices ![]()
tales que ![]() se cumple
que
se cumple
que
![]()
Así para tres sucesos ![]() serán independientes si se
cumple lo anterior , es decir, si
serán independientes si se
cumple lo anterior , es decir, si
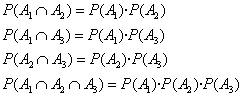
PROPIEDADES:
1.-Si A y B son independientes los complementarios también lo son.
Así Si A y B son independientes se cumplirá que

 para que
para que 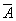 y
y ![]() sean
independientes deberá darse que
sean
independientes deberá darse que
![]()
Si 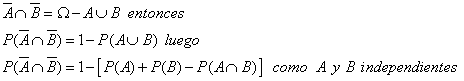
Entonces tendremos que : ![]() así
así
![]()
![]()
![]()
![]()
luego los complementarios son independientes
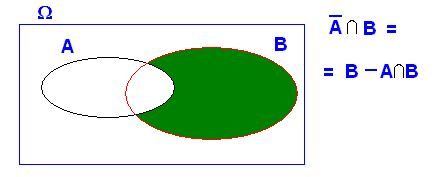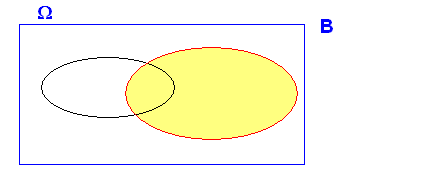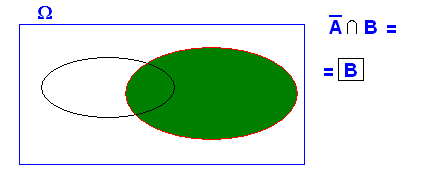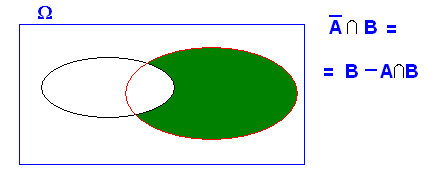
2.- Si A y B son independientes el complementario de A y el suceso de B también lo son. (evidentemente el complementarios de B y el suceso A , también)
Si A y B son independientes se cumplirá que

 para que
para que
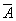 y
y ![]() sean
independientes deberá darse que
sean
independientes deberá darse que
![]()
ya que : ![]()
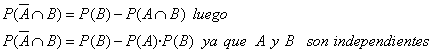
Así :
![]()
luego A
complementario y B son independientes.
Análogamente el complementario de B y el suceso A también serán independientes si A y B lo son
3.- Si A implica B ( A Í B) , A y B , “NO” son independientes
A y B son independientes si se cumple que

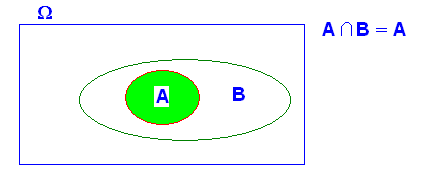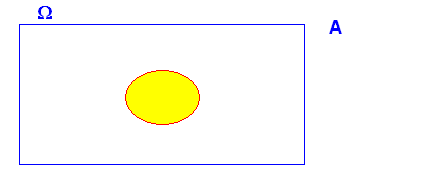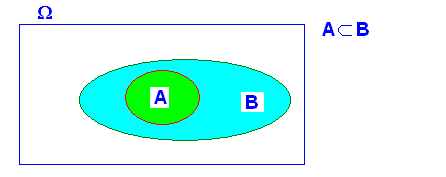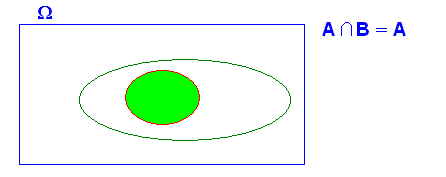 ya que
ya que ![]() luego
luego
![]() No
se cumple el teorema de caracterización
No
se cumple el teorema de caracterización
luego A y B No son independientes , salvo en el caso de que ![]()
en el que ![]() ; caso extremo e inadecuado
; caso extremo e inadecuado
4.-Si dos sucesos son incompatibles-disjuntos (mutuamente excluyentes o de intersección vacía), “NO” son independientes
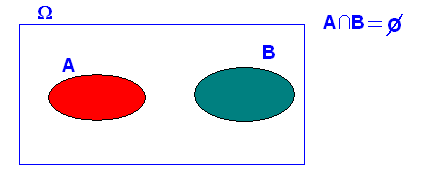 A y B son independientes si se cumple que
A y B son independientes si se cumple que

ya que ![]() luego
luego
![]() entonces
entonces
![]() No
se cumple el teorema de caracterización
No
se cumple el teorema de caracterización
luego A y B No son independientes , salvo que P(A) ó P(B) sean 0; caso
extremo e inadecuado