INDEPENDÈNCIA ESTOCÁSTICA DE SUCCESSOS:
Dos successos A i B són estocásticamente independents quan la informació sobre l'ocurrència d'un d'ells no modifica la probabilitat que ocorri l'altre.Això és:
P(A/B) = P(A) o equivalentment P(B/A) = P(B) exemple
CARACTERITZACIÓ DE LA INDEPENDÈNCIA: TEOREMA DE CARACTERITZACIÓ
A i B són independents Û P(AÇB) = P(A).P(B)
ja que si per definició d'independència 
i per definició de probabilitat condicionada 
haurà de complir-se que 
.
Així , dos successos A i B són independents si i
només si 
GENERALITZACIÓ DEL CONCEPTE D'INDEPENDÈNCIA (caracterització) PER A n SUCCESSOS
Un nombre finit o infinit de successos 
són mútuament
independents si daus els subíndices 
tals que 
es complix que
Així per a tres successos 
seran independents si
es complix l'anterior , és a dir, si
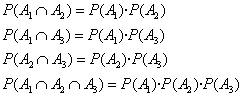
PROPIETATS:
1.-Si A i B són independents els complementaris també ho són.
Així Si A i B són independents es complirà que
perquè 
i 
siguin independents
haurà de donar-se que
Si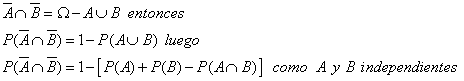 
Llavors hauríem de : 
així
després els complementaris són independents
2.- Si A i B són independents el complementari d'I el succés de B també ho són. (evidentment el complementaris de B i el succés A , també)
Si A i B són independents es complirà que
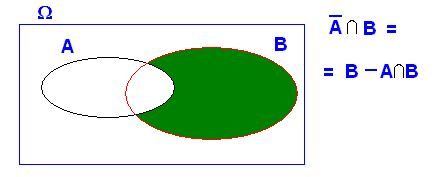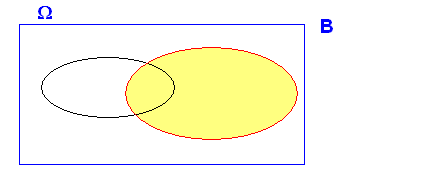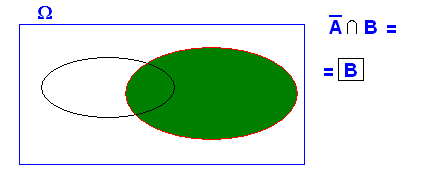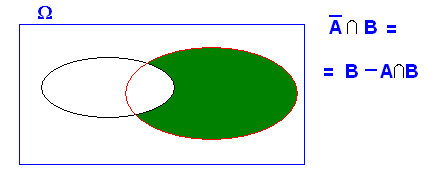perquè i 
siguin independents
haurà de donar-se que
ja que : 
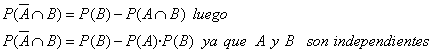
Així
: 
després A complementari i B són independents.
Anàlogament el complementari de B i el succés A també seran independents si A i B ho són
3.- Si A implica B ( A Í B) , A i B , “NO” són independents
A i B són independents si es complix que
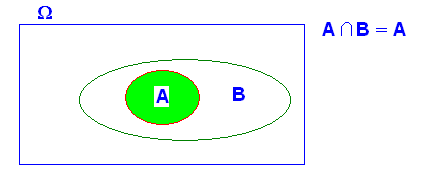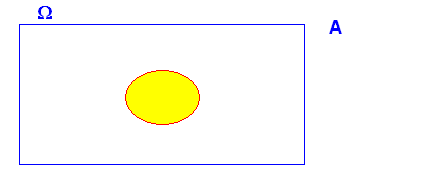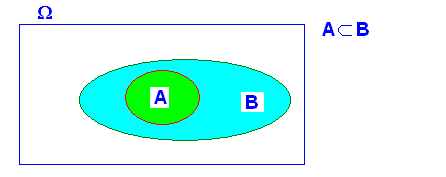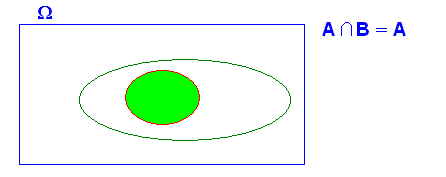ja que 
després
No
es complix el teorema de caracterització
després A i B No són independents , salvo en el cas que 
en el qual 
; cas extrem i inadequat
4.-Si dos successos són incompatibles-disjuntos (mútuament excloents o d'intersecció buida), “NO” són independents
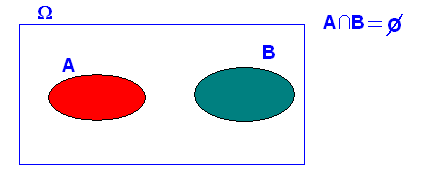A i B són independents si es complix que
ja que 
després
llavors
No
es complix el teorema de caracterització
després A i B No són independents , tret que P(A) o P(B) siguin 0; cas
extrem i inadequat