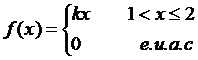
|
|
|
|
Determinar k perquè la funció f(x) puga ser una funció de probabilitat contínua.
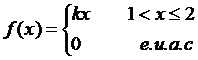
Com hem recordat en l’exemple anterior, les condicions que ha de satisfer una funció per poder ser de probabilitat són la no negativitat (f(x) ³ 0) i l’acumulació a 1. En aquest cas, en virtut de la continuïtat de la variable, cal expressar la segona condició –derivada de l’axioma segon de la probabilitat (P(W) = 1)–, en forma d’integral:
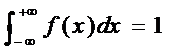
La suma s’estén a tota la recta real. Com que la funció f(x) pren diferents expressions en els diversos intervals, la integral es transforma en:
![]()
Resolent la integral:
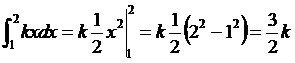
Per satisfer l’axioma segon de la probabilitat, aquesta darrera expressió s’ha d’igualar a la unitat i per tant:
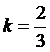
Com que k > 0, també queda satisfeta la primera condició f(x) ³ 0.

