EJEMPLO DE MUESTREO

Muestreo Irrestricto de tamaño 2

Comentario:

Al tratarse de un muestreo irrestricto de tamaño dos no hay reemplazamiento del primero dato muestral extraido. Así pues la distribución del primer dato muestral no se verá afectada por ello y seguirá siendo la de la población; pero la distrución del segundo dato muestral dependerá del primer dato muestral extraido: así tendermos una distribución del segundo dato muestral condicionada a que el primero haya sido el valor:

Teniendo en cuenta la distribución de la muestra  obedecerá a la expresión P(X1,X2)=P(X1).P(X2/X1).

Y a partir de la distribución de la muestra podremos obtener la distribución de la media muestral ,y sus características esenciales, esperanza y varianza.

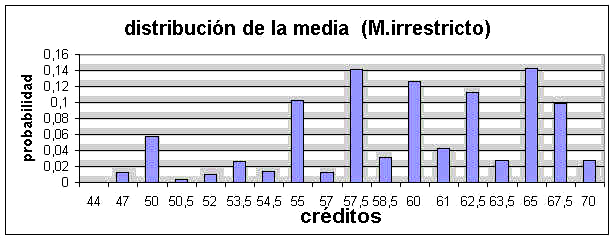
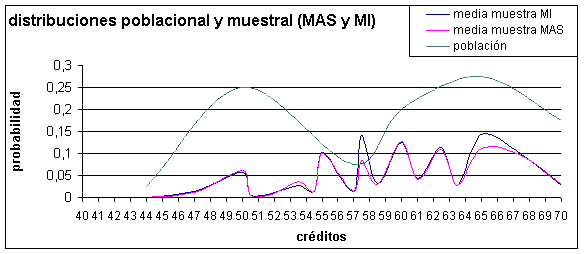
Tambien puede verse  el histograma de la distribución de la media muestral (irrestricta) y la comparación gráfica entre la distribución de la población, la de la media ( MAS) y la de la media (MI)

 

X1 FREC. PROB DISTRIBUCIÓN DEL PRIMER DATO MUESTRAL

El primer dato muestral no se ve afectado por el tipo de muestreo y así la distribución del priemr dato muestral coincide con la distribución de la población
44 1 0,025
50 10 0,25
57 3 0,075
60 8 0,2
65 11 0,275
70 7 0,175
TOTAL 40 1

 

DISTRIBUCIÓN DEL 2º DATO MUESTRAL / X1= 44    
     
X2/X1=44 FREC. P(X2/X1=44)
44 0 0
50 10 0,2564103
57 3 0,0769231

60

 8 0,2051282
65 11 0,2820513
70 7 0,1794872
  39 1

 

DISTRIBUCIÓN DEL 2º DATO MUESTRAL / X1= 50    
     
X2/X1=50 FREC. P(X2/X1=50)
44 1 0,025641
50 9 0,2307692
57 3 0,0769231
60 8 0,2051282
65 11 0,2820513
70 7 0,1794872
  39 1

 

DISTRIBUCIÓN DEL 2º DATO MUESTRAL / X1= 57    
     
X2/X1=57 FREC. P(X2/X1=57)
44 1 0,025641
50 10 0,2564103
57 2 0,0512821
60 8 0,2051282
65 11 0,2820513
70 7 0,1794872
  39 1

 

DISTRIBUCIÓN DEL 2º DATO MUESTRAL / X1= 60    
     
X2/X1=60 FREC. P(X2/X1=60)
44 1 0,025641
50 10 0,2564103
57 3 0,0769231
60 7 0,1794872
65 11 0,2820513
70 7 0,1794872
  39 1

 

DISTRIBUCIÓN DEL 2º DATO MUESTRAL / X1= 65    
     
X2/X1=65 FREC. P(X2/X1=65)
44 1 0,025641
50 10 0,2564103
57 3 0,0769231
60 8 0,2051282
65 10 0,2564103
70 7 0,1794872
  39 1

 

DISTRIBUCIÓN DEL 2º DATO MUESTRAL / X1= 70    
     
X2/X1=70 FREC. P(X2/X1=70)
44 1 0,025641
50 10 0,2564103
57 3 0,0769231
60 8 0,2051282
65 11 0,2820513
70 6 0,1538462
  39 1

Distribución de la muestra irrestricta y de la media muestral (M.I. n=2)

DISTRIBUCIÓN DE LAS POSIBLES MUESTRAS DE TAMAÑO n=2 ( M.IRRESTRICTO)
muestra

Mi=(x1,x2)

 media muestral

   probabilidad

P(x1,x2)=

=P()

    
 
x1 x2 media i P(x1) P(x2/x1)

P(x1,x2)

 .P() P()
44 44 44 0,025 0 0 0 1936 0
44 50 47 0,025 0,2564103 0,006410256 0,301282051 2209 14,16025641
44 57 50,5 0,025 0,0769231 0,001923077 0,097115385 2550,25 4,904326923
44 60 52 0,025 0,2051282 0,005128205 0,266666667 2704 13,86666667
44 65 54,5 0,025 0,2820513 0,007051282 0,384294872 2970,25 20,94407051
44 70 57 0,025 0,1794872 0,004487179 0,255769231 3249 14,57884615
50 44 47 0,25 0,025641 0,006410256 0,301282051 2209 14,16025641
50 50 50 0,25 0,2307692 0,057692308 2,884615385 2500 144,2307692
50 57 53,5 0,25 0,0769231 0,019230769 1,028846154 2862,25 55,04326923
50 60 55 0,25 0,2051282 0,051282051 2,820512821 3025 155,1282051
50 65 57,5 0,25 0,2820513 0,070512821 4,054487179 3306,25 233,1330128
50 70 60 0,25 0,1794872 0,044871795 2,692307692 3600 161,5384615
57 44 50,5 0,075 0,025641 0,001923077 0,097115385 2550,25 4,904326923
57 50 53,5 0,075 0,2564103 0,019230769 1,028846154 2862,25 55,04326923
57 57 57 0,075 0,0512821 0,003846154 0,219230769 3249 12,49615385
57 60 58,5 0,075 0,2051282 0,015384615 0,9 3422,25 52,65
57 65 61 0,075 0,2820513 0,021153846 1,290384615 3721 78,71346154
57 70 63,5 0,075 0,1794872 0,013461538 0,854807692 4032,25 54,28028846
60 44 52 0,2000 0,025641 0,005128205 0,266666667 2704 13,86666667
60 50 55 0,2000 0,2564103 0,051282051 2,820512821 3025 155,1282051
60 57 58,5 0,2000 0,0769231 0,015384615 0,9 3422,25 52,65
60 60 60 0,2000 0,1794872 0,035897436 2,153846154 3600 129,2307692
60 65 62,5 0,2000 0,2820513 0,056410256 3,525641026 3906,25 220,3525641
60 70 65 0,2000 0,1794872 0,035897436 2,333333333 4225 151,6666667
65 44 54,5 0,275 0,025641 0,007051282 0,384294872 2970,25 20,94407051
65 50 57,5 0,275 0,2564103 0,070512821 4,054487179 3306,25 233,1330128
65 57 61 0,275 0,0769231 0,021153846 1,290384615 3721 78,71346154
65 60 62,5 0,275 0,2051282 0,056410256 3,525641026 3906,25 220,3525641
65 65 65 0,275 0,2564103 0,070512821 4,583333333 4225 297,9166667
65 70 67,5 0,275 0,1794872 0,049358974 3,331730769 4556,25 224,8918269
70 44 57 0,175 0,025641 0,004487179 0,255769231 3249 14,57884615
70 50 60 0,175 0,2564103 0,044871795 2,692307692 3600 161,5384615
70 57 63,5 0,175 0,0769231 0,013461538 0,854807692 4032,25 54,28028846
70 60 65 0,175 0,2051282 0,035897436 2,333333333 4225 151,6666667
70 65 67,5 0,175 0,2820513 0,049358974 3,331730769 4556,25 224,8918269
70 70 70 0,175 0,1538462 0,026923077 1,884615385 4900 131,9230769
          1 E()=60   E()= 3627,501282

Esperanza y varianza y la media muestral 

(Muestreo irrestricto)

E( ) = media (población) =m= 60
Var ( )= (Var (población)/ n )(N-n/N-1)= (s2/n)(N-n/N-1)=27,501282
Var ( media muestral)=Var ()=E()-[E( )]2=

=3627,50128- (602)=27,501282

 

histomi.gif (25905 bytes)

 

grafconj.gif (28194 bytes)