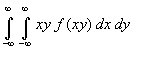COVARIANZA Y CORRELACIÓN ENTRE VARIABLES ALEATORIAS

La covarianza entre dos v.a. X e Y se define como:

            s _xy= E[(x-m _x)(y-m _y)] = E[x.y] - m _xm _y

                siendo E[x.y] el momento ordinario mixto de orden 1,1 ( a_1,1):

                    E[xy]=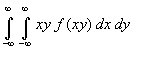 caso continuo

                        E[xy]=S S xy P(xy) caso discreto

La covarianza nos informa de la covariación conjunta de las dos variables, análogamente a como ocurría en el caso de distribuciones de frecuencias.Sólo hay que considerar aquí que la covariación hay que entenderla en términos de probabilidad y no de frecuencia: una covariación positiva sería el que a valores altos de una de la variables le corresponden "con mayor probabilidad" valores altos de la otra y a valores bajos valores bajos.(Una covariación negativa , inversamente).

Al igual también que en el caso de las distribuciones de frecuencias puede obtenerse un indicador de la correlación
( covariación estandarizada, relativizada y que permite la comparación al estar acotada):

Se define, entonces el coeficiente de correlación como: r =r _xy=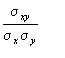

                    Indicador que viene a tener al mismo sentido que en las distribuciones de frecuencias y que igualmente está acotado entre -1 y 1.

Si dos variables aleatorias son estocásticamente independientes su coeficiente de correlación ( y su covarianza es cero).

Sin embargo el resultado recíproco no es necesariamente cierto (dos variables incorrelacionadas no tienen porqué ser independientes, por lo general)