exemple distribució de freqüències

REF.

Disposem a la taula següent d’informació sobre l’evolució dels preus (p) i les quantitats (q) intercanviades de tres productes 1, 2 i 3, al llarg de tres anys.

Taula 6.3

® Bé	1		2		3
¯ Any	p	q	p	q	p	q
2002	4	4	4	5	6	1
2003	4	5	5	8	9	1
2004	5	4	6	10	9	2

A partir d’aquestes dades, i triant sempre com a període base l’any 2002, calcular les següents sèries d’índexs de preus:

a) simples

b) Sauerbeck

c) Bradstreet-Dutot

d) Laspeyres

e) Paasche

f) Edgeworth

a) Començarem calculant els índexs simples

Taula 6.4

® Bé ¯ Any	1	2	3
2002	100	100	100
2003	100	125	150
2004	125	150	150

b) Amb la informació de la taula anterior podem calcular els índexs de preus de Sauerbeck

Taula 6.5

Any	Operació	*S_02,t*
2002		100
2003		125
2004		141.7

c) Per als valors de la taula 6.3, l’índex de Bradstreet-Dutot és:

Taula 6.6

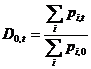
Any	Operació	D_02,t
2002		100
2003		128.6
2004		142.9

d) L’índex de Laspeyres pot ser presentat d’una manera alternativa com a mitjana d’índexs simples ponderats per als valors totals del període base ():

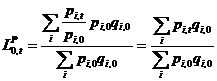
El càlcul de l’índex de preus de Laspeyres per als béns de la taula 6.3.

Taula 6.7

Any	Operació
2002		100
2003		119
2004		140.5

e) També l’índex de Paasche pot ser expressat com una mitjana aritmètica ponderada dels índexs simples de cada producte. Els pesos utilitzats són els valors totals del conjunt de béns produïts o intercanviats en el període actual, però valorats a preus unitaris del període base:

Taula 6.8

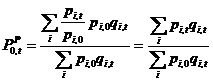
Any	Operació
2002		100
2003		119
2004		144.2

f) L’índex d’Edgeworth és una mitjana agregativa ponderada per la mitjana de les quantitats dels períodes base i corrent:

Taula 6.9

Any	Operació
2002		100
2003		119