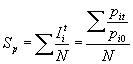
NUMÉROS ÍNDICES DE PRECIOS
NO PONDERADOS
ÍNDICE DE SAUERBECK
ÍNDICE DE BRADSTREET-DUTOT
PONDERADOS
ÍNDICE DE LASPEYRES
ÍNDICE DE PASCHE
ÍNDICE DE FISHER
ÍNDICE DE EDGEWORTH
EJEMPLO NÚMEROS INDICES DE PRECIOS PONDERADOS
PROPIEDADES DE LOS NÚMEROS ÍNDICES
CUMPLIMIENTO DE PROPIEDADES
Números índices de precios.
Son números índices evaluados para magnitudes precios.
Índices de precios no ponderados: Dado un conjunto de artículos:
Índice de Sauerbeck: de precios es la
media aritmética de los índices simples (de precios) de cada artículo:
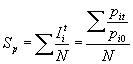
Índice de Bradstreet-Dûtot : es la media
agregativa de los precios: 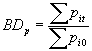
Ejemplo: Obtener los índices de precios de Sauerbeck y de Bradstreet-Dûtot para el conjunto de productos agrícolas : Arroz, trigo y patatas:
| Arroz | Trigo | Patatas | Arroz | Trigo | Patatas | I.Sauerbeck | I.B-Dûtot | |
| Periodo | Precio | Precio | Precio | I.Simple | I.Simple | I.Simple | (M-aritm.) | (M.agreg.) |
0 |
50 |
30 |
40 |
1 |
1 |
1 |
1 |
1 |
1 |
60 |
30 |
40 |
1,2 |
1 |
1 |
1,06666666 |
1,08333333 |
2 |
70 |
35 |
45 |
1,4 |
1,1666 |
1,125 |
1,23055555 |
1,25 |
3 |
75 |
40 |
45 |
1,5 |
1,3333 |
1,125 |
1,31944444 |
1,33333333 |
4 |
80 |
45 |
50 |
1,6 |
1,5 |
1,25 |
1,45 |
1,45833333 |
5 |
90 |
50 |
50 |
1,8 |
1,6666 |
1,25 |
1,57222222 |
1,58333333 |
Índices de precios ponderados
Dependiendo de las ponderaciones para cada bien (o articulo) y del tipo de promedio que se utilice se podrán generar distintos índices:
Índice de Laspeyres : Es la media aritmética ponderada de los índices simples de cada articulo utilizándose como ponderación para cada bien: wi = pi0.qi0 , esto es la ponderación para cada artículo será el valor de la cantidad consumida o vendida o producida del bien i-simo en el período base al precio del período base.
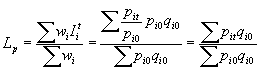
Índice de Pasche: Es la media aritmética ponderada de los índices simples de cada articulo utilizándose como ponderación para cada bien: wi=pi0.qit , esto es,el valor a precio del período base de la cantidad consumida en el período actual.
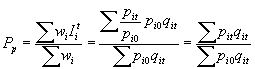
Índice de Fisher: Es simplemente la media geométrica de los dos anteriores.
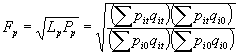
Índice de Edgeworth: Es la media agregativa ponderada de los índices simples de precios de cada artículo, utilizando como ponderación wi=qi0+qit Es decir, la suma de las cantidades consumidas, producidas o vendidas de cada artículo en el año baso y en el corriente :
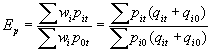
Ejemplo números índices ponderados
