|
|
|
|
REF.
I -1
Sean dos rectasde regresión X= 4-Y
6Y=20 -4X
sabiendo además que a20 =20
a) Determina cuál de ellas es la regresión de Y/X y cuál es la de X/Y (recuérdese que b.b`= R2.
b) Determinar las medias de X, Y
c)Obtener el coeficiente de correlación, la covarianza y la varianza de X y de Y
a) existen dos posiblidades :
1) Y/X : X=4 - Y , al tiempo que X/Y: 6Y=20 -4X
2) X/Y: X=4 - Y , al tiempo que Y/X: 6Y=20 -4X
Despejando adecuadamente tenemos:
en el primer caso
| Y/X | X/Y |
| Y=a+bX | X=a'+b' Y |
| Y= 4-X | X= 5 -3/2 Y |
| b = -1 | b' = 3/2 |
| b.b´= (-1).(-3/2)= 1'5 > 1 : así que no es posible | |
en el segundo caso:
| Y/X | X/Y |
| Y=a+bX | X=a'+b' Y |
| Y=(10/3)-(2/3)X | X= 4-Y |
| b = -2/3 | b' = -1 |
| b.b´= (-2/3).(-1)= 0`666 < 1 : así que Sí es posible | |
b) una vez determinadas las dos rectas de regresión: Y/X: 6Y=20 -4X , al tiempo que X/Y: X=4 - Y y teniendo en cuenta que las medias de X e Y satisfacen conjuntamente la ecuación de las dos rectas tendremos que :
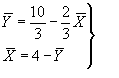y despejando:
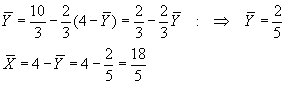
c) el coeficiente de correlación será, en primer lugar NEGATIVO, ya que los dos coeficientes de regresión lo son, y en segundo lugar :
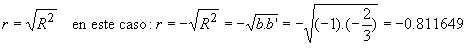
por otro lado de la expresión de cálculo de la varianza de X tenemos que:
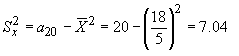
y de la expresión del coeficiente de regresión de la recta Y/X podemos despejar el valor de la covarianza:
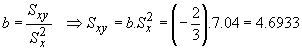
por último, la varianza de Y puede despejarse de la expresión del coeficiente de correlación, o de la del coeficiente de regresión de la recta X/Y:
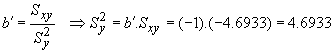
PROYECTO
CEACES
