problema unidimensionales I-7

I -7 Un grupo de 60 adolescentes tienen unos gastos semanales expresados en euros tal como se indican en la tabla:

X	n
20	5
35	10
50	30
65	10
80	5
	60

Obtener el gasto medio la varianza , ver si la distribución es simétrica y analizar su curtosis

Para resolver el problema podemos reducir la complejidad aritmética de los cálculos realizando un cambio (lineal) de variable (un cambio de origen y de unidad ). Estos cambios afectarán a la media y a la varianza pero no a los coeficientes de asimetría y de curtosis.

Si hacemos el cambio: ( y por lo tanto ) una vez obtenidas la media y la varianza de u tendremos que :

y

Procedamos:

u	n	un	u²	u²n	u³	u³n	u⁴	u⁴n
-2	5	-10	4	20	-8	-40	16	80
-1	10	-10	1	10	-1	-10	1	10
0	30	0	0	0	0	0	0	0
1	10	10	1	10	1	10	1	10
2	5	10	4	20	8	40	16	80
	60	0		60		0		180

De forma que:

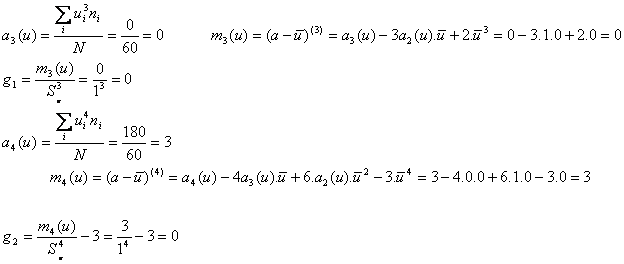
y por lo tanto la media y la varianza de la variable original (los gastos ) quedarán como:

el coeficiente de asimetría y el de curtosis serían invariantes y por lo tanto ambos iguales a cero

Con los valores originales los cálculos darían como resultado :

x	n	xn	x²	x²n	x³	x³n	x⁴	x⁴n	Media	50
20	5	100	400	2000	8000	40000	160000	800000	a²	2725
35	10	350	1225	12250	42875	428750	1500625	15006250	S²	225
50	30	1500	2500	75000	125000	3750000	6250000	1,88E+08	S	15
65	10	650	4225	42250	274625	2746250	17850625	1,79E+08	a₃	158750
80	5	400	6400	32000	512000	2560000	40960000	2,05E+08	m₃	0
	60	3000		163500		9525000		5,87E+08	g₁	0
									a₄	9776875
									m₄	151875