REF.

    I -6    Una máquina fabricó placas de titanio para el Guggenheim  a un coste  de  1000 euros cada una . Las fabricaba con una holgura al alza entre 0 y 8 cm .Siendo la holgura una variable aleatoria . La holgura de la pieza ( siempre a mayor) no podía sobrepasar los 6 cm. ,las placas con mayor holgura no se podía utilizar y por tanto vender, pero si tenían un valor residual de 500 euros. Las placas útiles se vendían a 1500 cada una . Si para revestir la obra de Gerhy se fabricaron 20000 placas, calcular el beneficio esperado de la empresa que fabricó el revestimiento, conociendo que la holgura tenía una función de densidad f(x)=x/32.

función de beneficio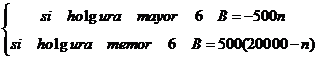      

PD = número de piezas desperdiciadas de una , variable aleatoria

PD = 0 es que la holgura es menor que 6

PD =1 es que la holgura es mayor que 6

                                       E[PD] = 0·P(x<6)+1·P(x>6)=0,437

                     P(x>6)=P(holgura mayor que 6)=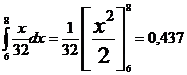

                         n = número de piezas desperdiciadas de 20000= 20000·PD

                       E[B]= -500E[n]+500(20000-E[n])

                       E[n]= 20000· E[PD]=8740

                                  Luego E[B] = -4370000+5630000=1260000 euros

?