REF.

    II -9  Un lote consiste en 10 piezas de longitud x . Dicha longitud es una variable aleatoria con
función de densidad 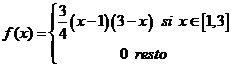      metros

Un lote es correcto si nueve de sus piezas son válidas , es decir , su longitud esté comprendida entre 1,7 y 2,4 metros. Si hemos adquirido 4 lotes . Calcular la probabilidad de que más de dos de ellos sean correctos.

y =ínúmero de lotes correctos de 4ý  ¿ P(y>2)=P(y=3)+P(y=4)

                    yÞB(4, p)   siendo p = P( lote válido )

 Si v =ínúmero de piezas válidas de 10ý 

                   v ÞB(10,p₁ )   siendo p₁  = P( pieza válida)

P(pieza válida)=

                        luego  v ÞB(10,0,502 )   P( lote válido ) = P ( v ³ 9)=P(v = 9)+P(v =10)

                                                        por lo que    p= P(lote válido )= 0,011

          Tendremos así que : y Þ B(4; 0,011)   como nos interesa

                                                                                         P( y>2)=P(y=3)+P(y=4)

           Por lo que la probabilidad pedida sería  P( y>2)=P(y=3)+P(y=4)=0,000005001

?