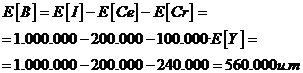REF.

    III -8  La distribución de fallos de un equipo que se emplea en un proceso productivo sigue una ley exponencial y el equipo tiene según las especificaciones técnicas , una vida útil media de 10 horas . Si para llevar acabo con éxito el proceso de producción hace falta que trabaje ininterrumpidamente 24 horas .

a)¿Cuál es la probabilidad de conseguirlo sin tener que reemplazar el equipo?

b) Si el coste de reposición del equipo es de 100.000 u.m , y conocemos que en el proceso de producción completo(24 horas) se genera un producto valorado en 1.000.000 um. Con unos costes de explotación de 200.000 . Determinar el beneficio esperado en un proceso productivo.

a)       conocemos la media  

establecemos también que :   X≡ vida útil en horas del equipo

de donde   X®Exp ( a )    donde a = 0,1  ya que   

Nos piden  P (equipo aguante más de 24 horas ) = P( X > 24)

b)  Beneficio = I – Ce-Cr   donde los Ingresos son fijos = 1.000.000 , los costes de explotación son fijos = 200.000  y los Costes de reposición dependen del número de veces que se reponga el equipo (Y) . Así.

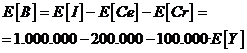
Siendo Y el número de veces que se (repone) se estropea el equipo en 24 horas

Luego   ; siendo X≡ vida útil en horas del equipo y por tanto X®Exp ( a=0,1 )

De donde :       luego:

?