REF.
I -6 Se ha comprobado que el peso de un paquete sigue una
ley normal . Los controles de calidad revelaron que un tercio de los paquetes pesaban
menos de 870 gr y que sólo dos de cada mil paquetes pesaban más de 1 kg. . Calcular .
a) La probabilidad de que si elegimos un paquete al azar éste pese más de 850 gr.
b) Si en una semana salen al
mercado 40000 paquetes ¿Cuántos cabe esperar que pesen mas de 900 gr. ?
a) Para resolver
las preguntas a y b necesitamos conocer la distribución (parámetros) del peso P del
paquete.
Para ello si :P(P<870)=0,33 luego en
normal[0,1]
siendo t1 el valor negativo (dado que la probablidad es menor que 0,5 ) de el
valor que
siendo este 0,4307 es
decir t1 real -0,4307
Conocemos también que 2 de cada mil pesan más de 1000 luego P(P>1000)=0,002 luego en
la tipificada
por lo que
por tablas tendremos que t2 = 2,878 .Destipificando y resolviendo el sistema :
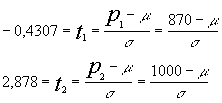resolviendo el sistema m =886,9 y s =39,29
luego el peso del paquete será P : N[886,9 ;39,29] luego
b) la proporción de paquetes con más 900 gr. será :
dado que tenemos 40000 paquetes que han de pesar más 900 o no estaremos ante una N= número de paquetes que pesan más de 900 que será una B(40000 ;0,369)
se nos pregunta cuantos "cabe esperar" luego será la esperanza matemática E[N]=np=40000·0,369=14760
