REF.

    II -1     En un espacio probabilístico se consideran los sucesos  A y C cuyas  probabilidades  son  P(A) = 0,3 y P(B) = 0,6.  Por B^c se designa el suceso complementario o contrario al suceso B. Calcular la probabilidad del suceso A∩ B^c en los siguientes casos:

a)      La probabilidad del suceso A∩B es 0,2.

b)      Los sucesos A y B son independientes

Selectividad Universidad de Valencia.

                 Si observamos la figura resulta:

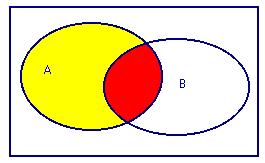
                                                                       La zona roja, sombreado del centro, es la intersección de A y B, es decir, A∩ B

                                                                       La zona amarilla, sombreado de la izquierda, es la intersección de A y del complementario de B, es de , A∩ B^c

                                                                      Además, la unión de las dos zonas es A, es decir, (A∩ B^c)U(A∩ B)=A

                                                     Aplicando probabilidad y dado que son disjuntos

                                                     P(A∩ B^c)+P(A∩ B) = P(A), ya que se trata de dos sucesos incompatibles.

                                                      Y despejando en la igualdad anterior, p(A∩ B^c) = p(A) – p(A∩ B)

·         En el primer caso, P(A∩ B) = 0,2

P(A∩ B^c) = 0,3 – 0,2 = 0,1

·         En el segundo caso los sucesos son independientes, por tanto,

P(A∩ B) = P(A).P(B) = 0,3.0,6 = 0,18

y entonces, P(A∩ B^c) = 0,3 – 0,18 = 0,12

?