EJERCICIO (ejemplo) 2 SERIES TEMPORALES
DETERMINACIÓN DE LA TENDENCIA DE UNA SERIE TEMPORAL REF.
Dada la siguiente serie del número de alumnos universitarios para el período 1979-1999:
|
Curso |
Alumnos |
|
1979-80 |
657.447 |
|
1980-81 |
649.098 |
|
1981-82 |
669.848 |
|
1982-83 |
692.152 |
|
1983-84 |
744.115 |
|
1984-85 |
788.168 |
|
1985-86 |
854.104 |
|
1986-87 |
902.284 |
|
1987-88 |
969.412 |
|
1988-89 |
1.027.018 |
|
1989-90 |
1.093.086 |
|
1990-91 |
1.140.572 |
|
1991-92 |
1.209.108 |
|
1992-93 |
1.291.996 |
|
1993-94 |
1.358.616 |
|
1994-95 |
1.445.322 |
|
1995-96 |
1.505.611 |
|
1996-97 |
1.551.969 |
|
1997-98 |
1.568.752 |
|
1998-99 |
1.583.297 |
Fuente: Hasta 1991-92, Anuario de Estadística Universitaria 1993/1994 Desde 1992-93 hasta 1996-97, Estadística Universitaria del curso 1996-97 (Datos provisionales) Desde 1997-98 hasta 1998-99, Web del Instituto Nacional de Estadística
Obtener la tendencia de la serie:
a) Mediante el método de las medias móviles a tres años.
b) Mediante el método de ajuste a una función lineal.
Yt, número de alumnos universitarios en el curso t.
a)
La primera media móvil corresponde al curso 1980-1981 (t=2) y se calcula como:
![]()
La siguiente media móvil será:
![]()
La serie completa de medias móviles será:
|
Curso |
t |
|
|
1979-80 |
1 |
- |
|
1980-81 |
2 |
658.797’7 |
|
1981-82 |
3 |
670.366’0 |
|
1982-83 |
4 |
702.038’3 |
|
1983-84 |
5 |
741.478’3 |
|
1984-85 |
6 |
795.462’3 |
|
1985-86 |
7 |
848.185’3 |
|
1986-87 |
8 |
908.600’0 |
|
1987-88 |
9 |
966.238’0 |
|
1988-89 |
10 |
1.029.838’7 |
|
1989-90 |
11 |
1.086.892’0 |
|
1990-91 |
12 |
1.147.588’7 |
|
1991-92 |
13 |
1.213.892’0 |
|
1992-93 |
14 |
1.286.573’3 |
|
1993-94 |
15 |
1.365.311’3 |
|
1994-95 |
16 |
1.436.516’3 |
|
1995-96 |
17 |
1.500.967’3 |
|
1996-97 |
18 |
1.542.110’7 |
|
1997-98 |
19 |
1.568.006’0 |
|
1998-99 |
20 |
- |
Al aplicar el método de las medias móviles a 3 puntos se ha perdido información, puesto que no se puede determinar la tendencia de la primera y de la última observación de la serie. La tendencia de la serie será la línea que une las medias móviles y que se puede ver en el gráfico situado al final del apartado b).
b)
Se trata de efectuar el siguiente ajuste que asume un comportamiento lineal para la tendencia:
![]() ,
es decir, que el origen está situado en el primer año de la serie.
,
es decir, que el origen está situado en el primer año de la serie.
Los cálculos a realizar para la obtención de los parámetros a y b se encuentran en la siguiente tabla:
|
|
t’ |
yt’ |
t’2 |
yt’×t’ |
|
|
|
|
0 |
657.447 |
0 |
0 |
4.3224×1011 |
548.968’2 |
|
|
1 |
649.098 |
1 |
649.098 |
4.2133×1011 |
605.403’0 |
|
|
2 |
669.848 |
4 |
1.339.696 |
4.4870×1011 |
661.837’8 |
|
|
3 |
692.152 |
9 |
2.076.456 |
4.7907×1011 |
718.272’6 |
|
|
4 |
744.115 |
16 |
2.976.460 |
5.5371×1011 |
774.707’4 |
|
|
5 |
788.168 |
25 |
3.940.840 |
6.2121×1011 |
831.142’2 |
|
|
6 |
854.104 |
36 |
5.124.624 |
7.2949×1011 |
887.577’0 |
|
|
7 |
902.284 |
49 |
6.315.988 |
8.1412×1011 |
944.011’8 |
|
|
8 |
969.412 |
64 |
7.755.296 |
9.3976×1011 |
1.000.446’6 |
|
|
9 |
1.027.018 |
81 |
9.243.162 |
1.0548×1012 |
1.056.881’4 |
|
|
10 |
1.093.086 |
100 |
10.930.860 |
1.1948×1012 |
1.113.316’1 |
|
|
11 |
1.140.572 |
121 |
12.546.292 |
1.3009×1012 |
1.169.750’9 |
|
|
12 |
1.209.108 |
144 |
14.509.296 |
1.4619×1012 |
1.226.185’7 |
|
|
13 |
1.291.996 |
169 |
16.795.948 |
1.6693×1012 |
1.282.620’5 |
|
|
14 |
1.358.616 |
196 |
19.020.624 |
1.8458×1012 |
1.339.055’3 |
|
|
15 |
1.445.322 |
225 |
21.679.830 |
2.0890×1012 |
1.395.490’1 |
|
|
16 |
1.505.611 |
256 |
24.089.776 |
2.2669×1012 |
1.451.924’9 |
|
|
17 |
1.551.969 |
289 |
26.383.473 |
2.4086×1012 |
1.508.359’7 |
|
|
18 |
1.568.752 |
324 |
28.237.536 |
2.4610×1012 |
1.564.794’5 |
|
|
19 |
1.583.297 |
361 |
30.082.643 |
2.5068×1012 |
1.621.229’3 |
|
å |
190 |
21.701.975 |
2470 |
243.697.898 |
2.5699×1013 |
|
|
1/Nå |
9’5 |
1.085.098’75 |
123’5 |
12.184.894’9 |
1.2850×1012 |
|
Utilizando los resultados obtenidos en la tabla anterior:
|
|
|
|
|
|
|
|
|
de donde se obtiene que:
![]()
![]()
Por lo que, la tendencia queda definida por:
![]()
A partir de esta ecuación de tendencia y dando valores a t’=0,1,2,...,19, se obtienen estimaciones de la tendencia para cada año de la serie que se encuentran recogidas en la última columna de la tabla anterior. Hay que observar que, a diferencia del método de las medias móviles, no se han perdido observaciones.
Además, este método de obtención de la tendencia nos permite medir la bondad del ajuste efectuado mediante el coeficiente de determinación que, al ser un ajuste lineal, coincide con el cuadrado del coeficiente de correlación lineal. Esto es:
![]()
Al ser el valor de R2 bastante próximo a uno, el ajuste lineal para la tendencia es válido.
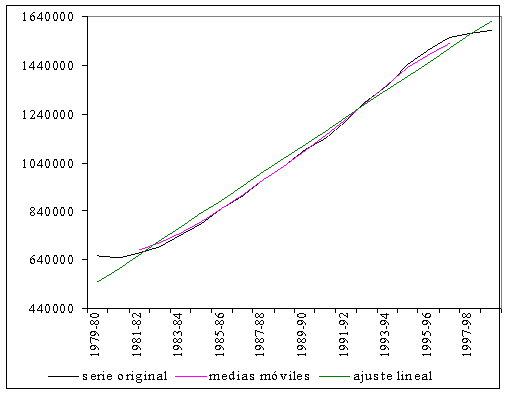
En el siguiente gráfico pueden verse representadas tanto la serie original de la evolución de los estudiantes universitarios como las dos series de tendencia obtenidas en los apartados a) y b).
Gráfico: Tendenia de la Serie del número de alumnos universitarios para el periodo 1979-1999.