EJERCICIO(ejemplo) 3 SERIES TEMPORALES
Obtener los índices de variación estacional trimestrales
y desestacionalizar la siguiente serie de entrada de
visitantes (en miles de personas) en España, suponiendo un esquema de
combinación multiplicativo y estacionalidad estable.
|
|
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
|
Trimestre 1 |
8.829.990 |
9.388.445 |
10.561.137 |
10.951.676 |
11.937.650 |
12.252.737 |
|
Trimestre 2 |
14.002.528 |
14.656.385 |
15.873.035 |
17.634.452 |
18.467.791 |
19.313.746 |
|
Trimestre 3 |
20.980.878 |
21.773.563 |
23.790.177 |
25.490.256 |
26.807.345 |
27.407.366 |
|
Trimestre 4 |
10.593.634 |
11.451.005 |
12.190.628 |
13.685.449 |
14.847.505 |
15.437.562 |
Fuente:
FRONTUR,
I.N.E.
Sea 
la variable que
representa el número de visitantes de España, en miles de personas, en el año t.
Recordemos que
bajo un esquema de combinación multiplicativo las fluctuaciones de la serie
vienen determinadas por 
.
PROCEDIMIENTO:
1º:
Hallamos la tendencia de la serie
2º:
Eliminamos la tendencia
3º:
Eliminamos las variaciones irregulares
4º:
Expresamos las Variaciones Estacionales en forma de
índices: Indices de Variación Estacional
(IVE)
1º Hallamos la
tendencia de la serie. Para ello, calculamos la ecuación lineal de la tendencia
anual con origen en 1995 y tomando como valores de la serie los totales anuales
del número de visitantes: 
, donde 
en 1995.
|
Años |
t |
|
|
|
|
|
1995 |
0 |
54.407.030 |
0 |
0 |
2'9601×1015 |
|
1996 |
1 |
57.269.398 |
1 |
57.269.398 |
3'2798×1015 |
|
1997 |
2 |
62.414.977 |
4 |
124.829.954 |
3'8956×1015 |
|
1998 |
3 |
67.761.833 |
9 |
203.285.499 |
4'5917×1015 |
|
1999 |
4 |
72.060.291 |
16 |
288.241.164 |
5'1927×1015 |
|
2000 |
5 |
74.411.411 |
25 |
372.057.055 |
5'5371×1015 |
|
|
15 |
388.324.940 |
55 |
1.045.683.070 |
2'5457×1016 |
A partir de la tabla anterior se obtiene que
En
consecuencia, la ecuación de tendencia anual con origen en 1995 queda definida
por:
La bondad del
ajuste se obtiene mediante el coeficiente de determinación:
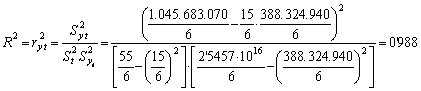
por lo que el ajuste
lineal es muy adecuado.
La ecuación de
la tendencia trimestral con origen en el trimestre central del año 1995 tendrá
por expresión
donde 
expresa, ahora,
trimestres.
Cambiamos el
origen de la ecuación de tendencia trimestral para situarlo en el primer
trimestre de 1995, que se corresponde con el valor 
.
Puesto que
la ecuación de tendencia trimestral
con origen en el primer trimestre de 1995 es:
A partir de la
ecuación anterior evaluamos la tendencia para cada uno de los 24 trimestres de
la serie original, sustituyendo 
. Los valores obtenidos para la tendencia se recogen en la
siguiente tabla.
|
|
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
|
Trimestre 1 |
13.105.158 |
14.174.740 |
15.244.322 |
16.313.904 |
17.383.485 |
18.453.067 |
|
Trimestre 2 |
13.372.554 |
14.442.136 |
15.511.717 |
16.581.299 |
17.650.881 |
18.720.462 |
|
Trimestre 3 |
13.639.949 |
14.709.531 |
15.779.113 |
16.848.694 |
17.918.276 |
18.987.858 |
|
Trimestre 4 |
13.907.345 |
14.976.926 |
16.046.508 |
17.116.090 |
18.185.672 |
19.255.253 |
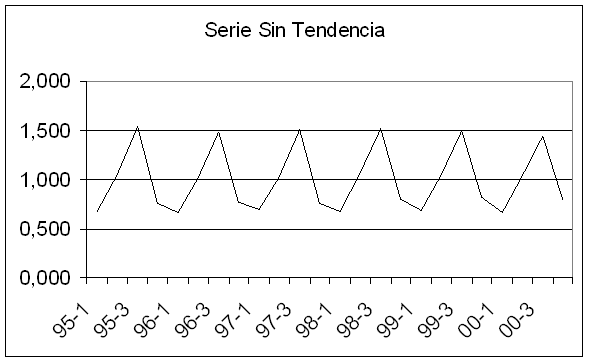
2º Eliminamos
la tendencia de la serie dividiendo los datos originales por su correspondiente
valor de tendencia, dado que suponemos un esquema de combinación de las
componentes, multiplicativo. La serie corregida, sin tendencia, es la
siguiente.
|
|
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
|
Trimestre 1 |
0'674 |
0'662 |
0'693 |
0'671 |
0'687 |
0'664 |
|
Trimestre 2 |
1'047 |
1'015 |
1'023 |
1'064 |
1'046 |
1'032 |
|
Trimestre 3 |
1'538 |
1'480 |
1'508 |
1'513 |
1'496 |
1'443 |
|
Trimestre 4 |
0'762 |
0'765 |
0'760 |
0'800 |
0'816 |
0'802 |
3º Eliminamos las variaciones irregulares sobre
la estacionalidad efectuando promedios trimestrales. Los movimientos estacionales pueden medirse a través de las medias
aritméticas para cada trimestre (suponemos estacionalidad estable). La
expresión de los movimientos estacionales en forma de
porcentaje recibe el nombre de índices de variación estacional y representa el
efecto estacional para cada trimestre. Al suponer estacionalidad estable, son
los mismos para todos los años de la serie:
|
|
|
|
|
|
Trimestre 1 |
4'051 |
0'675 |
67'62 |
|
Trimestre 2 |
6'227 |
1'038 |
103'98 |
|
Trimestre 3 |
8'978 |
1'496 |
149'86 |
|
Trimestre 4 |
4'705 |
0'784 |
78'54 |
|
|
|
3'993 |
400 |
Los índices de
variación estacional pueden ser interpretados de la siguiente manera: el efecto
estacional en el 1er trimestre hace que el número de entradas de
visitantes sea un 
inferior al nivel
normal que es 100. De forma análoga, la influencia estacional produce en el 3er
trimestre una entrada de visitantes un 49'86% superior respecto al nivel
normal.
4ª Eliminamos
la estacionalidad de la serie dividiendo los datos originales entre los IVE de
cada trimestre, expresados en tantos por uno. La serie desestacionalizada está
recogida en la siguiente tabla:
|
|
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
|
Trimestre 1 |
13.058.252 |
13.884.125 |
15.618.363 |
16.195.912 |
17.654.022 |
18.119.990 |
|
Trimestre 2 |
13.466.559 |
14.095.389 |
15.265.469 |
16.959.465 |
17.760.907 |
18.574.482 |
|
Trimestre 3 |
14.000.319 |
14.529.269 |
15.874.935 |
17.009.379 |
17.888.259 |
18.288.647 |
|
Trimestre 4 |
13.488.202 |
14.579.838 |
15.521.553 |
17.424.814 |
18.904.386 |
19.655.668 |
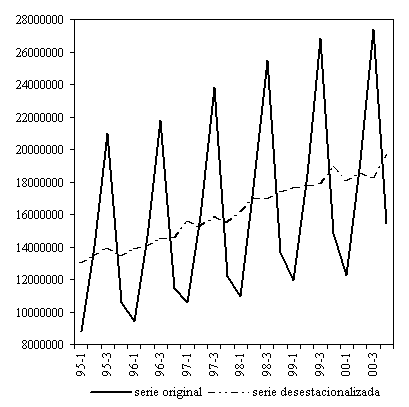
Esta serie desestacionalizada indica qué valores hubiésemos observado
de no haber existido la influencia estacional. Al contrario de lo que ocurre
con la serie original, cuando los datos están desestacionalizados
se puede apreciar como en algunos años la entrada de visitantes en el 4º
trimestre ha sido superior a la del 3er trimestre.
En el siguiente
gráfico se encuentran representadas tanto la serie original de entrada de
visitantes en España (en miles) como la correspondiente serie desestacionalizada.
