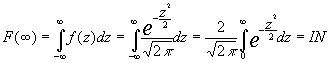
3.1.Comprobación de que la distribución Normal Reducida es una distribución de probabilidad

La función de densidad es siempre positiva por lo que bastará  para probar que puede ser una distribución de probabilidad con el hecho de comprobar que su función de distribución toma el valor 1 en el infinito: es decir F(¥ )=1

                Así                  

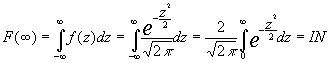
Conocemos por otra parte que la integral impropia (integral de Poisson) es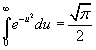 

siendo ,evidentemente , U una función de z.

     por lo que realizando el cambio       por lo que   y

                    tendremos que la integral que buscamos resolver será:

                                                              
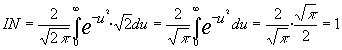
                            por lo que se demuestra que es función de distribución de probabilidad.