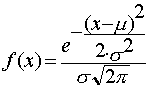
2. La distribución Normal general (ir a normal)
Como se ha dicho ,depende de dos parámetros , m , s , que como luego comprobaremos , son su media y su desviación típica .
El hecho de que una variable x se distribuya con una distribución normal de media m y desviación típica s se representa por:
X ® N[m
;s ] ó L(X)®
N[m ;s ]
(Aunque nosotros seguiremos este sistema de especificación , es bastante corriente ,
también ‚ que a la distribución normal se la especifique por los parámetros media
y varianza ( en vez de desviación típica), m , s 2
Su función de densidad es:
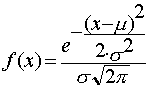
![]()
Las características de dicha función de densidad serán:
Si realizamos la primera derivada de dicha función tendremos que :
dado que : 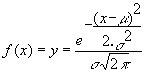
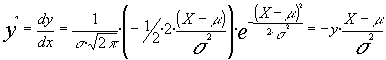
la segunda derivada será: 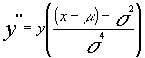
Igualando a cero la primera derivada obtenemos que y'=0 para X = m y para X = ¥ .
Como la segunda derivada en x = m es negativa ,concluimos que la función de densidad presenta un máximo en X = m , lo que nos hace afirmar que la media ( m ) es también la moda de la distribución normal.
Es fácil comprobar que la función de densidad presenta dos puntos de
inflexión en los valores X = ![]()
Por otro lado para cualquier valor de a se verifica que: ¦ (m +a)= ¦ (m -a) por lo que la función es simétrica respecto a m
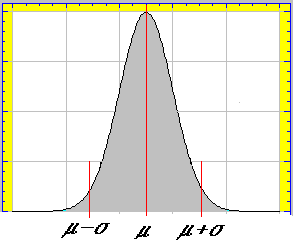
Teniendo en cuenta estos resultados la representación gráfica de la función de densidad resultaría de la siguiente manera: