DISTRIBUCIONES MUESTRALES PARA UNA POBLACIÓN NORMAL
De todas las posibles distribuciones básicas es ,sin duda ,la distribución normal la más importante por el gran número de poblaciones que se distribuyen así, real o asintóticamente ,(en virtud de los Teoremas Límite).
Así pues ,en los subapartados siguientes ,consideraremos que conocemos la distribución de la población y que ‚ ésta , es normal . Consideraremos igualmente muestreo aleatorio simple (m.a.s.)
DISTRIBUCIÓN DE LA MEDIA MUESTRAL
Si la población se distribuye
N[m ;s ]
entonces
en efecto si 
y dado que 
siendo independientes pues realizamos m.a.s. y en aplicación del teorema fundamental de
las distribuciones normales obtendremos
DISTRIBUCIÓN DE LA VARIANZA MUESTRAL
En lugar de obtener la distribución muestral del estadístico varianza muestral
L [S2] que nos llevaría a
conclusiones próximas a las anteriormente descritas en el apartado en el que la
población no era normal, es más conveniente la utilización de la variable aleatoria
que recordemos , no es un estadístico , y que contiene en su expresión a la varianza
muestral y a la poblacional , de ahí su utilidad dado que ambas quedan relacionadas con
una distribución conocida ; la jhi-dos.
No demostramos la relación pero la recordamos dada su importancia posterior.
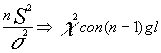
DISTRIBUCIÓN DE LA MEDIA MUESTRAL CON VARIANZA DESCONOCIDA
En apartados anteriores estudiamos el comportamiento de la media muestral y vimos que ésta dependía tanto del valor de la media poblacional , como de la varianza poblacional , parece lógico pensar que si nuestro interés radica en inferir comportamientos de la población partiendo de la muestra parece ilógico pensar que conozcamos la varianza . De ahí la importancia de establecer una distribución para la media muestral que la relacione únicamente con la poblacional , lo que hará que conocida la muestral concreta podamos aventurar el comportamiento de la poblacional.
Así tendríamos :
lo que da
lugar a :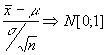 
hemos visto sin demostrar que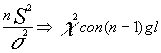
conocemos que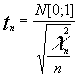 
luego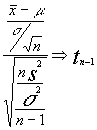 
simplificando tendríamos
expresión que relaciona ambas medias y la varianza muestral con una distribución conocida