ir a construcción de intervalos

ir a script de realización

Las circunstancias específicas para la construcción de este intervalo son las siguientes :

              Intervalo para el cociente de dos varianzas poblacionales

            Realizamos dos muestras aleatorias simples de tamaños n y m

            De dichas muestras se extraen las varianza muestrales

Conocemos que las poblaciones 1 y 2 para cuya razón de varianzas queremos construir el intervalo son Normales.

Lógicamente prefijamos un nivel de confianza de 1-a .

Conocemos según vimos cuando estudiamos las distribuciones muestrales de  normales que :

por el lema de Fisher - Cochran      :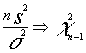
para las dos poblaciones que tenemos se dará .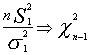          y   :  
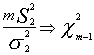
      nótese que el tamaño muestral de la muestra de 1ª es n y la de 2ª  es m

                      dado que nos interesa la razón de varianzas y en aplicación de la expresión de la F de Snedecor:

tendremos 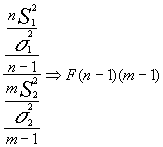                         arreglando el cociente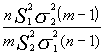

dado que nos interesa el cociente inverso        tendríamos que:

                                                                                   
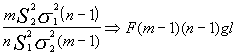
                                                donde esta incluida la razón de varianzas para la cual queremos crear un intervalo .

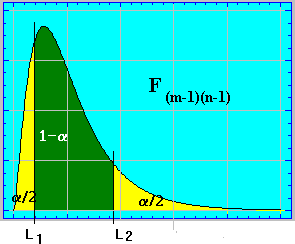
Si hemos establecido un nivel de confianza de 1-a el intervalo para una F(m-1)(n-1) vendría dado por las constantes L₁ y L₂ , adoptándose el criterio simplificador ,próximo al de mayor longitud , de considerar:

de manera que y por otra parte :

                                una vez determinados los valores de L₁ y L₂ tendríamos el intervalo       
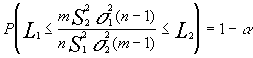                                   despejando la razón que nos interesa tendríamos :   
                                                     

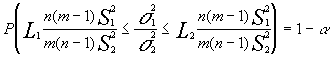
Evidentemente si plantemos medir la diferencia entre las varianzas , cuanto más próximo se la razón a la unidad menor diferencia habrá entre las varianzas y lógicamente cuando la razón entre estas difiera mucho de 1 ,la diferencia entre varianzas será mas ostensible.