INTERVALO DE COFIANZA PARA LA MEDIA DE UNA POBLACIÓN CUALQUIERA CON VARIANZA CONOCIDA    ir a esquema

ir a intervalos

ir a script de realización

Las circunstancias específicas para la construcción de este intervalo son las siguientes :

Intervalo para m
Conocida s ( o la varianza )
Distribución poblacional desconocida.
Nivel de confianza dado 1-a
Tamaño muestral desconocido luego nos colocamos en el peor de los casos , es decir pequeño.

                 Partiendo del conocido teorema de Markov :        

                    donde g(x) es una función cualquiera de la variable aleatoria x , y dicha función g está definida NO negativa,
siendo c una constante cualquiera. Así :

                       definiendo            g(x)= 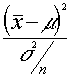      es , evidentemente , no negativa

                                       y tomando     c=H²         tendremos en aplicación de Markov :

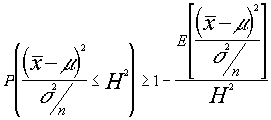                                 dado que :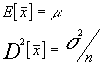    

     tendremos que                  

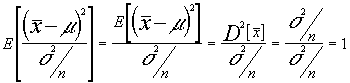
                                                    transponiendo este resultado al enunciado general :

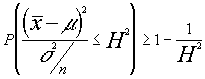                                          tomando la raíz cuadrada tendremos

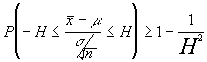                                         despejando para centrar el parámetro a estimar m

si queremos establecer un nivel de confianza 1-a igualaremos éste a  d e manera que     por lo que en función del nivel de confianza el intervalo quedaría :

ejemplo 1

En población cuya distribución se desconoce se obtiene una muestra (m.a.s.) de 2000 valores de la que resulta una media de 225 y una desviación típica de 10 . Suponiendo que la varianza muestral coincide con la poblacional , estimar un intervalo para la media de la población con un nivel de confianza del 95%.

Tendríamos 1-a =0.95       luego a =0.05 ;       S=10=s  ;     n=2000 ; 
                    con    

           aplicando                       con más de 0.95 de confianza.

ir a programa de realización (script)