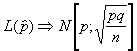ir a construcción de intervalos

ir a script con m.a.s  y p=conocida
ir a script con m.a.s  y p=q=0.5
ir a script con irestricto y p=conocida
ir a scrpt con irrestricto y p=q=0.5

Deseamos estimar la proporción con la que se da una característica en una determinada población , esta característica es dicotómica por lo que o bien se posee o bien no . El intervalo se plantea , como todos con un nivel de confianza 1-a prefijado. Realizando , claro está, un muestreo de tamaño n , que en principio consideramos aleatorio simple.

Del estudio de las distribuciones conocemos el comportamiento de la proporción con la que una característica se da en la muestra : así 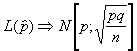siendo p la proporción con la que la característica aparece en la población ;
                    "q"    lógicamente su complementario y   n el tamaño muestral .

                         Tipificando obtendríamos :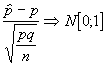

Como en los casos anteriores y dado que utilizamos la N[0,1] ; para un nivel de confianza dado ,1-a , los valores de dicha normal que generan un intervalo centrado corresponderían a       por lo que quedaría el siguiente intervalo :

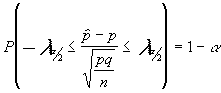                                             despejando la proporción poblacional :

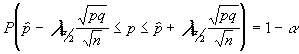
                                                    que es intervalo que estabamos buscando .

En el caso de que el muestreo fuera irrestricto su expresión sería , tras aplicar el f.c.p.f., la siguiente :

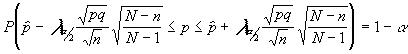
Como se ha podido comprobar en ambas expresiones de intervalo está contenida y por tanto es necesaria para su construcción la proporción poblacional "p" .Parece ilógico que si queremos estimar dicha proporción la conozcamos y por tanto la podamos utilizar . El problema puede resolverse de varias formas según el caso :

• Si el tamaño muestral es muy grande podríamos utilizar como proporciones poblacionales las obtenidas por la muestra ; es decir tomar en lugar de pq . Evidentemente si el intervalo se pre-construye antes de que se realice la muestra (por ejemplo para calcular el tamaño muestral necesario para un determinado error , como veremos después) este no será el método aconsejable .

• En el caso de poseer información "fiable" de la proporción de la población , bien por estimaciones anteriores recientes , bien por pre-muestreos (piloto) , podríamos utilizar dichas estimaciones como los valores reales de p y por tanto de q=1-p.
• Lo más habitual , para resolver este problema , consiste en "colocarse" en la situación más desfavorable posible en cuanto a los valores de dicha proporción poblacional. Dicha situación no es otra que valorar p=q=0.5 ,con lo que se consigue establecer como cierta la máxima varianza en la población (es fácil demostrar que dadas las características de p y q el máximo de p·q se obtiene precisamente con p=q=0.5). Adoptando esta medida ,en la construcción del intervalo, se consigue que la amplitud de éste sea mayor, menos precisa, y por tanto para una misma amplitud necesitará un mayor tamaño de la muestra que el realizado con otra p , pero resuelve el problema del desconocimiento de p y augura , al darse mayor amplitud , más "fiabilidad". (obsérvese que en casi-todas las encuestas de opinión la ficha técnica incluye el mencionado p=q=0.5) .

ejemplo 4

En una investigación comercial se muestrea a 100 individuos resultando que 25 de ellos han comprado nuestro producto .Dar un intervalo para la proporción de penetración en el mercado con una probabilidad (nivel de confianza) del 95 % .

       conocemos :

               1-a = 0.95 ; n=100 (grande) proporción muestral =

                  el intervalo sería :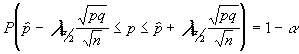
donde el valor de   = 1.96 según tabla N[0,1]  (ir a tabla de la normal)  y    0.95 de confianza.

Desconocemos la proporción poblacional p ; dos opciones

1. p= dado que la muestra es grande ; que aplicada en el intervalo daría que : la proporción de penetración en el mercado está entre el 16'51 % y el 33'48 % con una confianza del 95 % (ir a script de realización)

2. p=q=0.5 poniéndonos en el caso de varianza máxima ; en el caso por tanto más desfavorable. En este caso la proporción de penetración en el mercado estaría entre el 15.2% y el 34.8 con una confianza del 95% ; como se puede apreciar el intervalo tiene más holgura que el realizado por el método anterior. (ir a script de realización)