ir a intervalos

ir a script de realización con m.a.s
ir a script de realización con irrestricto
ir a esquema

Las circunstancias específicas para la construcción de este intervalo son las siguientes :

Intervalo para m
desconocida s ( o la varianza )dado que n es pequeña no podemos tomar S como s
Distribución poblacional normal.
Nivel de confianza dado 1-a
Tamaño muestral desconocido luego nos colocamos en el peor de los casos , es decir pequeño.

Del estudio de las distribuciones muestrales conocemos que :       

Como la distribución de t de student es una distribución simétrica , unimodal y centrada en 0 , de todos los intervalos que verifiquen que :                     P(t Î IN) = 1 - a el de menor amplitud será:

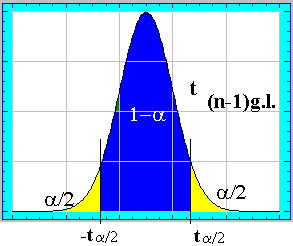
                donde     es el correspondiente valor de la variable t para n - 1 grados de libertad y nivel de significación a . Dicho intervalo quedaría :

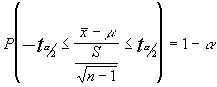para un nivel de confianza                     
                         prefijado y despejando tendríamos como intervalo

                                                                                                                                                                                                                   

recuérdese que en el caso de muestreo irrestricto sería de aplicación el antes nombrado factor corrector de poblaciones finitas.

ir a esquema

ejemplo 3

Las ventas diarias de cierta oficina comercial se supone que siguen una distribución normal. Para estimar el volumen medio de ventas por día se realiza una muestra de 10 días escogidos al azar ,resultando que la media de las ventas de esos 10 días es 100 u.m. con una desviación típica de 4 u.m. Dar un intervalo de estimación para el volumen medio de ventas por día con una confianza del 95 % . (ir a script de realización)

conocemos que  según la información que poseemos, estamos ante:

      normal ;   n=10  (muestra pequeña) ;  S=4(poblacional desconocida)  ;   media muestral=100 ;

        1-a =0.95     luego a =0.05     con lo que       (según tabla)(ir a tabla de la t)

                     y dado que el intervalo a utilizar (nada dicen de irrestricto ; luego m.a.s) será

                                   resultando :

                                                   µ Î [96'99;103'01] con el 95 % de confianza