TEST DE KRUSKAL WALLIS PARA LA COMRACIÓN DE VARIAS MUESTRAS INDEPENDIENTES

ir a contrastes no paramétricos

Este contraste, debido a Kruskal y Wallis, viene a ser una generalización del test de Mann-Whitney para el caso de k muestras independientes.Se examina la hipótesis de que estas muestras provengan de la misma población o de poblaciones de idéntico comportamiento, frente a la alternativa de que no todas provienen de la misma población. En este sentido es una versión "no parámetrica" del Análisis de la Varianza. Este test, al igual que el de Mann-Whitney presenta una muy alta eficiencia ( o potencia relativa ).Siendo más potente que otras pruebas no paramétricas similares como la de la mediana.

La situación de aplicación es tal que disponemos de k muestras independientes de tamaños: n₁,n₂,...,n_k con n₁+ n₂+...+ n_k = n donde estas observaciones están medidas en, al menos escala ordinal.(ordenación)

Si llamamos R_i a la suma de los rangos de las observaciones de la i-sima muestra el estadístico H:

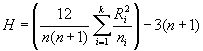
sigue aproximadamente una distribución c² con k-1 grados de libertad:

De forma que, dado un nivel de significación,a,   si el estadístico evaluado,H, supera el valor crítico, c²_a(k-1) rechazaremos la hipótesis nula de que las muestras provienen de poblaciones iguales.

ir script de realización para tres muestras
ir script de realizción para cuatro muestras

ir a tests basados en la ordenación