1. Un determinado estadístico J se distribuye según un modelo jhi-dos de parámetro (grados de libertad) 14 . Deseamos saber la probabilidad con la que dicho estadístico tomará un valor menor que 9,467.

J® nos preguntan por directamente de la tabla será 0,2

2. Otro estadístico se distribuye según una c 2 con 20 grados de libertad ¿Cuál será el valor de dicho estadístico para el que se genera un nivel de significación del 0,05 % ?

O® dado que nos piden el valor de la variable O será ;
o lo que es lo mismo directamente en tablas 31,41

3. Dada una variable aleatoria que se distribuye como una t de Student con 16 grados de libertad .
a)Calcular la probabilidad de que dicha variable tome valores menores que 1.071 .
b)Calcular la probabilidad de que dicha variable( en valor absoluto) tome valores menores que 1.071.
c)Conociendo que la probabilidad de que la variable en valor absoluto sea superior a un valor (crítico) es 0,1   Calcular dicho valor crítico .

Conocemos que         X 

a)        directamente en tablas será 0,85

b)      dado que es en valor absoluto será el área entre -1,071 y 1,071 luego el resultado será
                           F(1,071)-(1-F(1,071)=0,85-(1-0,85)=0,7

c)   conociendo que

             esto será la probabilidad de que la variable tome valores superiores a X1 o inferiores a - X1    
luego 0,1 es la suma de las "colas" de la t.(cada una de valor 0,05) luego el valor de X1  según tablas será 1,725

4. Una variable se distribuye como una F de Snedecor de parámetros 3  y   7 . Calcular la probabilidad de que dicha variable tome valores superiores a 8,45 .

            se nos pregunta por directamente en tabla  tendremos que =0,01

5. El ratio comercial A se distribuye según una N[12,4] um. Y el ratio B como otra normal de media 10 y varianza 25 , Entre ambos ratios existe una correlación de 0,8 . Según estudios realizados el mejor indicador económico que debemos utilizar es uno tal cuya estructura es R=5A+2B+1.
a)Calcular la probabilidad de que dicho ratio R tome el valor 83 .
b)Calcular la probabilidad de que R tome valores superiores a 84 .

a)           

                R=5A+2B+1 combinación lineal de normales no independientes luego

                   

                 R será Normal luego    así   podremos calcular probabilidades para R

P(R=83)=imposible ó 0   ;  R es una distribución normal , por tanto continua , luego los valores concretos no existen por lo que es imposible calcular la probabilidad para un valor concreto.

b)     P(R>84) =  0,4

6. Una pieza tiene de longitud L que es normal de media 10 cm. y varianza 0,1 cm. al cuadrado . Se le lija 1 cm. que evidentemente no es preciso y perfecto lo es más o menos según una normal de media 1 cm y desviación 0,1 cm . Una pieza es buena si su longitud está comprendida entre 8,8 y 9,2 cm .Si preparamos 10 piezas ¿Cuál es la probabilidad de que al menos 9 de ellas sean buenas ?

 

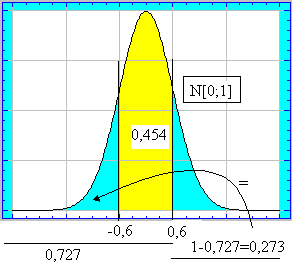
es la longitud al principio se procede al lijado que es

luego la longitud final será

 

siendo una combinación lineal de normales independientes luego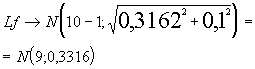

                                               
                                 la proporción o probabilidad de que la pieza sea buena será

               

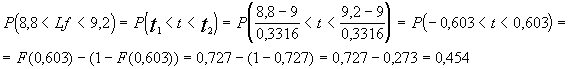
7.El número de personas que compran en una tienda es aleatorio , pero por término medio se supone que este número es de 5 en una hora. Calcular la probabilidad de que en dos horas hayamos hecho exactamente 8 ventas.

El número de personas que compran ( C ) en una hora puede considerarse como una Poisson así :
C® para dos horas y por el teorema de adición para la distribución de Poisson (compran en 2 horas=2C)
2C®
la probabilidad de que en dos horas 8 ventas será     P(2C=8)=

8. Dos cadenas de montaje convergen a un único taller de acabado que durante cinco minutos trata a una sola unidad. El tiempo que las unidades están en cada cadena es aleatorio y con distribución normal. Independiente de una cadena a otra , con parámetros : cadena A ® N[12 ;4] . cadena B ® N[9 ;3] ambas en minutos
Si a las doce horas entra a la cadena A una unidad y ocho minutos después entra a la cadena B otra unidad.
a)¿ Cuál es la probabilidad de que la unidad de B llegue al taller de acabado antes que la unidad A ? 0,1587
b)¿Cuál es la probabilidad de que cuando llegue la unidad de B puede ser ésta tratada sin demora ?

tiempo en Cadena A A® N[12 ;4] minutos
tiempo en Cadena B B® N[9 ;3] minutos

B entra 8 minutos después que A así :

a) Los momentos de llegada serán
A® N[12 ;4] minutos
B® N[9+8 ;3] minutos                 la diferencia de tiempos de llegada será B-A

                                    B-A =dif® = =N[5 ;5]

                        B llegará antes si dif < 0       así

                        probabilidad de que llegue antes    P(dif < 0)  =P(dif < 0)=P(t < t1 )= P(t < -1) = 0.1587

b) La unidad B entra sin demora si la unidad A ya ha salido o bien si llega antes que la A.

así si el tiempo de B es el de A + 5 o si tiempo de B es menor que el de A

                    P(dif >5) È P( dif < 0) = P(t > t1) + 0.1587= P( t > 0) + 0.1587= 0.5+0.1587=0.6587

                    t1=(5-5)/5=0

9. Dada una variable aleatoria bidimensional (x ;y) con distribución normal bivariante de parámetros

m = v = determinar

a) P(1,5< x< 2,5) .
b)   siendo z=2x+y  calcular P(Z< 2)
c)  siendo z=2x-y   calcular P(z<2)

 

a) x ® N(2 ;2)   luego    P(1,5< x< 2,5) = P (t1 < t <t2) = P (-0.25<t<0.25) = 0.1974

siendo  t1= (1.5-2)/2=-0.25      t2= (2.5-2)/2=0.25

b) Z= 2x+y          Z® N[ 2·2+3 ; ] =     N[7 ; ]

            P(Z< 2) = P( t < t1 ) =P (t < -0.963)= 0.1685

       siendo       t1= (2-7)/5.19=-0.963

c) Z=2x-y               Z® N [2·2-3 ;]  =     N [1 ;]

                P(Z< 2) = P( t < t1 ) =P (t < 0.3)= 0.6179

         siendo    t1= (2-1)/3.31=0.3